Задача 60068 Найти общий интеграл дифференциального...
Условие
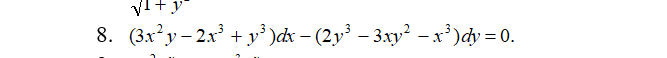
Решение
P(x;y)=3x^2y-2x^3+y^3 и Q(x;y)=2y^3-3xy^2-x^3 - однородные третьего порядка
или
[m]y`=\frac{3x^2y-2x^3+y^3}{2y^3-3xy^2-x^3}[/m]
Делим и числитель и знаменатель дроби справа на [m]x^3[/m]
[m]y`=\frac{3\frac{y}{x}-2+(\frac{y}{x})^3}{2(\frac{y}{x})^3-3(\frac{y}{x})^2-1}[/m]
Решается заменой
y/x=u
y=x*u
y`=x`*u+x*u`
x`=1, так как х независимая переменная
[m]u+x\cdot u`=\frac{3u-2+u^3}{2u^3-3u^2-1}[/m]
[m]x\cdot u`=\frac{3u-2+u^3}{2u^3-3u^2-1}-u[/m]
[m]x\cdot u`=\frac{3u-2+u^3-2u^4+3u^3+u}{2u^3-3u-1}[/m] - уравнение с разделяющимися переменными
[m]u`=\frac{du}{dx}[/m]
[m]x\cdot du=\frac{4u-2+4u^3-2u^4}{2u^3-3u^2-1}dx[/m]
Разделяем переменные:
[m] \frac{2u^3-3u^2-1}{4u-2+4u^3-2u^4}du=\frac{dx}{x}[/m]
Интегрируем:
[m] ∫ \frac{2u^3-3u^2-1}{4u-2+4u^3-2u^4}du= ∫ \frac{dx}{x}[/m]
[m] -\frac{1}{2} ∫ \frac{2u^3-3u^2-1}{u^4-2u^3-2u+1}du= ∫ \frac{dx}{x}[/m]
так как [m] d(u^4-2u^3-2u+1)=(u^4-2u^3-2u+1)`du=(4u^3-6u^2-2)du=2\cdot (2u^3-3u^2-1)du[/m] ⇒
[m](2u^3-3u^2-1)du=\frac{1}{2}d(u^4-2u^3-2u+1)[/m]
[m] -\frac{1}{2} ∫ \frac{\frac{1}{2}d(u^4-2u^3-2u+1)}{u^4-2u^3-2u+1}du= ∫ \frac{dx}{x}[/m]
[m]-\frac{1}{4}ln|u^4-2u^3-2u+1|=ln|x|+lnC[/m]
[m]ln|u^4-2u^3-2u+1|^{-\frac{1}{4}}=lnC|x|[/m] ⇒ [m](u^4-2u^3-2u+1)^{-\frac{1}{4}}=Cx[/m], где
[m]u=\frac{y}{x}[/m]
или
[m]\frac{1}{\sqrt[4]{(\frac{y}{x})^4-2(\frac{y}{x})^3-2(\frac{y}{x})+1}}=Cx[/m]