Задача 59596 ...
Условие
log(2x^2-x)*log4(3x^2-5x+6) ≥ 0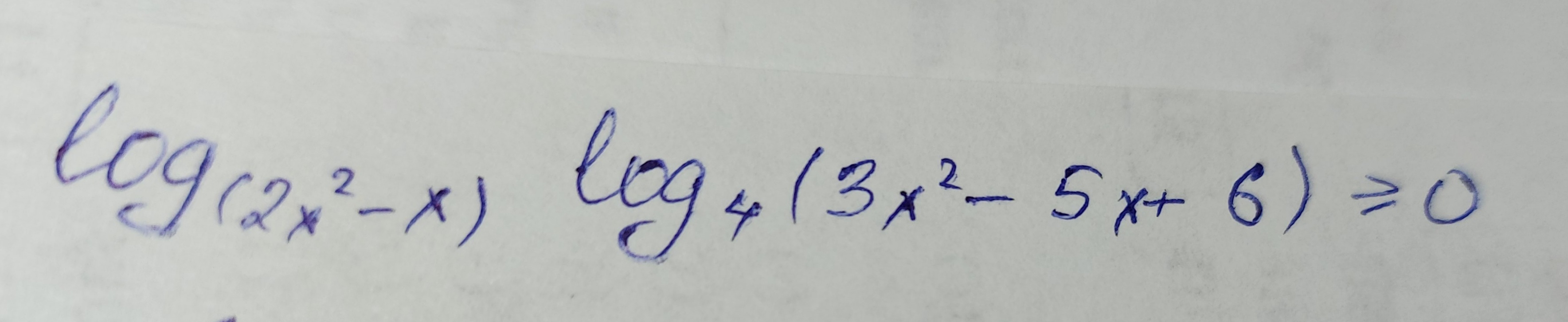
Решение
[m]\left\{\begin {matrix}2x^2-x>0\\2x^2-x ≠1\\3x^2-5x+6>0\\3x^2-5x+6 ≠ 1\\log_{4}(3x^2-5x+6)>0 \end {matrix}\right.[/m]
Так как [m]0=log_{a}1[/m], a >0; a ≠ 1, то
[m]log_{2x^2-x}log_{4}(3x^2-5x+6) ≥ log_{2x^2-x}1[/m]
Рассматриваем два случая:
1)
Если основание логарифмической функции [m]2x^2-x>1[/m], то функция [i]возрастающая[/i]
[m]\left\{\begin {matrix}2x^2-x>1\\log_{4}(3x^2-5x+6) ≥ 1 \end {matrix}\right.[/m]
2)
Если основание логарифмической функции [m]0<2x^2-x<1[/m], то функция [i]убывающая[/i]
[m]\left\{\begin {matrix}0<2x^2-x<1\\0<log_{4}(3x^2-5x+6) ≤ 1 \end {matrix}\right.[/m]
[m]1=log_{4}4[/m]
и учитывая, что логарифмическая функция с основанием 4 >1 [i] возрастающая[/i], получаем:
1)
[m]\left\{\begin {matrix}2x^2-x>1\\3x^2-5x+6 ≥ 4 \end {matrix}\right.[/m]
2)
[m]\left\{\begin {matrix}0<2x^2-x<1\\1<(3x^2-5x+6) ≤ 4 \end {matrix}\right.[/m]