Задача 58965 Решить при помощи правила Лопиталя....
Условие
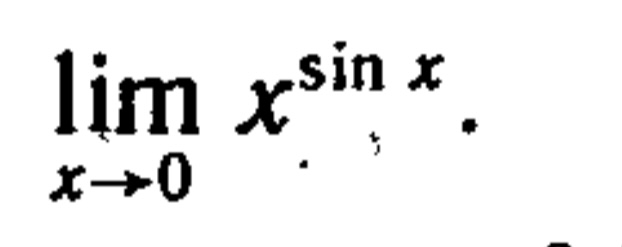
Решение
Логарифмируем:
lny=lnx^(sinx)
Применяем свойства логарифма степени:
lny=sinx*lnx
Тогда
lim_(x →0) lny=lim_(x →0) sinх*lnx=получили неопределенность 0* ∞
которая легко сводится к неопределенности (0/0) или ( ∞ / ∞ )
lim_(x →0) sinх*lnx=lim_(x →0)[m]\frac{sinх}{\frac{1}{lnx}}=[/m] (0/0)
lim_(x →0) sinх*lnx=lim_(x →0)[m]\frac{lnх}{\frac{1}{sinx}}=[/m] ( ∞ / ∞ )
А уже эти неопределенности считают по правилу Лопиталя
lim_(x →0)[m]\frac{sinх}{\frac{1}{lnx}}=[/m] lim_(x →0)[m]\frac{(sinх)`}{((lnx)^{-1})`}=[/m] lim_(x →0)[m]\frac{cosx}{(-1)\cdot ((lnx)^{-2})\cdot (lnx)`}=[/m] lim_(x →0)[m]\frac{cosx}{(-1)\cdot \frac{1}{ln^2x}\cdot \frac{1}{x}}=[/m] -lim_(x →0) (cosx*ln^2x*x) снова неопределенность [b]0* ∞[/b]
Значит, этот выбор не подходит
lim_(x →0)[m]\frac{lnх}{\frac{1}{sinx}}=[/m] lim_(x →0)[m]\frac{(lnх)`}{((sinx)^{-1})`}=[/m] lim_(x →0)[m]\frac{\frac{1}{x}}{(-1)\cdot \frac{1}{sin^2x}\cdot cosx}=[/m] -lim_(x →0)[m]\frac{sin^2x}{x\cdot cosx}=[/m]
А вот здесь все прилично:
[/m] -lim_(x →0)[m]\frac{sinx}{x}\cdot\frac{sinx}{cosx}=[/m]-1*0=0
О т в е т. lim_(x →0)y=e^(0)=1