Задача 57677 Поэтапно пожалуйста, вычислить интегралы...
Условие
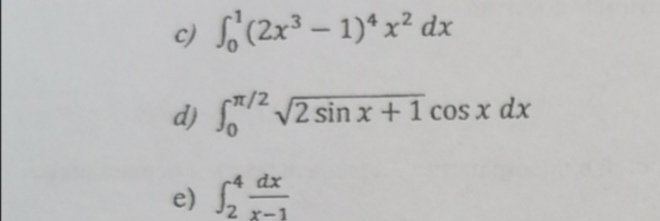
Решение
применяем метод замены переменной
[r][m] ∫ ^{b}_{a}f(u)du= ∫ ^{ β }_{ α }f( φ (x)) φ `(x)dx[/m]
[/r]
Смотрим на [i]правую[/i] часть формулы ( применение формулы справа налево называется
[i]подведением под дифференциал[i]. Этот способ освобождает от [b]замены[/b] пределов интегрирования)
Если выражение под интегралом содержит сложную функцию ( как в формуле справа)
[m]f( φ (x))[/m] и производную внутренней функции [m]φ `(x)[/m]
то пытаемся определить [m] φ (x)[/m] и [m]f[/m]
производная конечно же x^2, но от какой функции, от х^3.
Кубическая функция тоже есть: (это 2x^3-1). Все найдено.
Итак,
[red][m] φ (x)=2x^3-1[/m][/red] Тогда [red][m] φ`(x)=(2x^3-1)`dx=8x^2dx[/m][/red]
То, что нет множителя 8 - не страшно. НА ЧИСЛО всегда можно умножить и и разделить (вынести за знак интеграла)
Итак, решение имеет вид:
[m] ∫ ^{1}_{0}(2x^3-1)^4x^2dx=\frac{1}{8} ∫ ^{1}_{0}(2x^3-1)^4\cdot 8 x^3dx[/m][red]=[/red]
с 8 и (1/8) разобрались
Теперь с дифференциалом:
[m]d( φ (x))= φ `(x)dx[/m]
и[b] Обратно[/b][m] φ `(x)dx=d( φ (x))[/m]
[red]=[/red][m]\frac{1}{8} ∫ ^{1}_{0}(2x^3-1)^4\cdot d(2x^3-1)[/m][green]=[/green]
А это табличный интеграл: [m] ∫ ^{1}_{0}u^4du=\frac{u^5}{5}|^{1}_{0}[/m]
[green]=[/green][m]\frac{(2x^3-1)^5}{5}|^{1}_{0}=\frac{1}{5}-\frac{(-1)}{5}=\frac{2}{5}[/m]
d)
[red][m] φ (x)=2sinx+1[/m][/red] Тогда [red][m] φ`(x)=(2sinx+1)`dx=2cosx dx[/m][/red]
Недостает константы [b]2[/b]
[m] ∫ ^{\frac{π}{2}}_{0}\sqrt{2sinx+1} cosx dx=\frac{1}{2}∫ ^{\frac{π}{2}}_{0}\sqrt{2sinx+1}\cdot (2\cdot cosx) dx=\frac{1}{2}∫ ^{\frac{π}{2}}_{0}\sqrt{2sinx+1}d(2sinx+1)[/m][green]=[/green]
табличный интеграл [m] ∫ \sqrt{u}du=\frac{u^{\frac{3}{2}}}{\frac{3}{2}}[/m]
[green]=[/green][m]\frac{1}{2}\cdot \frac{(2sinx+1)^{\frac{3}{2}}}{\frac{3}{2}}| ^{\frac{π}{2}}_{0}=[/m]
[m]=\frac{1}{3}\cdot \sqrt{(2sinx+1)^3}|^{\frac{π}{2}}_{0}=\frac{1}{3}(\sqrt{3^3}-\sqrt{1^3})=\frac{1}{3}(3\sqrt{3}-1)=\sqrt{3}-\frac{1}{3}[/m]
e)
[m] ∫ ^{4}_{2}\frac{dx}{x-1}=∫ ^{4}_{2}\frac{d(x-1)}{x-1}=(ln|x-1|)|^{4}_{2}=ln(4-1)-ln(2-1)=ln3[/m]