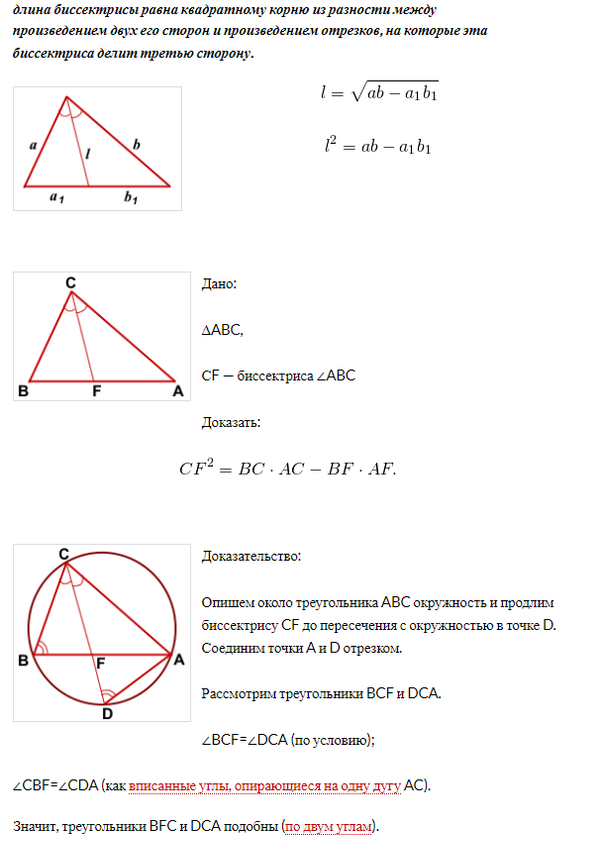
Задача 57271 Пусть в треугольнике ABC AC = b , BC = a...

5feac286960c3c35933d8141

22.01.2021 12:14:23

Пусть в треугольнике ABC AC = b , BC = a . Докажите, что для биссектрисы l c , проведенной из вершины C , имеет место формула l=sqrt(ab-c'c'') , где с' и c'' отрезки, на которые делит биссектриса противоположную сторону

5f3ea7e3faf909182968ddd9

22.01.2021 12:42:32

★

По теореме косинусов:

[m]c^2_{1}=a^2+l^2-2alcos φ [/m]; [m] 2φ = ∠ C[/m]

[m]c^2_{2}=b^2+l^2-2blcos φ [/m];


⇒ [m]\frac{a^2+l^2-c^2_{1}}{2al}=\frac{b^2+l^2-c^2_{2}}{2bl}[/m] ⇒


[m]\frac{a^2+l^2-c^2_{1}}{a}=\frac{b^2+l^2-c^2_{2}}{b}[/m] ⇒[m] b(a^2+l^2-c^2_{1})=a(b^2+l^2-c^2_{2})[/m] ⇒

[m]bl^2-al^2=ab^2-a^2b-bc^2_{1}+ac^2_{2}[/m]

[m]l^2\cdot (b-a)=ab(b-a)-bc^2_{1}+ac^2_{2}[/m]


По свойству биссектрисы:

[m]\frac{c_{1}}{c_{2}}=\frac{a}{b}[/m] ⇒ [m]bc_{1}=ac_{2}[/m]


[m]l^2\cdot (b-a)=ab(b-a)-bc_{1}\cdot c_{1}+ac_{2}\cdot c_{2}[/m]

[m]l^2\cdot (b-a)=ab(b-a)-ac_{2}\cdot c_{1}+bc_{1}\cdot c_{2}[/m]

[m]l^2\cdot (b-a)=ab(b-a)-c_{1}c_{2}\cdot (b-a)[/m]

[m]l^2=ab-c_{1}c_{2}[/m]