Задача 56691 Найти объем тела ограниченного...
Условие
Решение
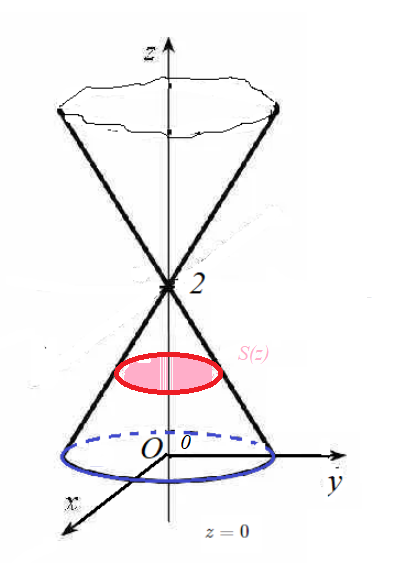
[m]V=∫^{2}_{0}S(z)dz[/m]
Где [m]S(z) [/m]- площадь сечения конуса плоскостями, параллельными плоскости хОу
В сечениях получатся эллипсы:
[m]\frac{x^2}{3}+\frac{y^2}{2}=(z-2)^2[/m] ⇒ [m]\frac{x^2}{3(z-2)^2}+\frac{y^2}{2(z-2)^2}=1[/m]
Площадь эллипса [m]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/m] равна [m]πab[/m]
Поэтому
[m]S(z)=π\cdot \sqrt{3}(z-2)\cdot \sqrt{2}(z-2)=\sqrt{6}π\cdot (z-2)^2[/m]
[m]V=∫^{2}_{0}\sqrt{6}π\cdot (z-2)^2dz=\sqrt{6}\cdot π\cdot (\frac{(z-2)^3}{3})|^{2}_{0}=\frac{8\sqrt{6}π}{3}[/m]
2.
Через двойной интеграл
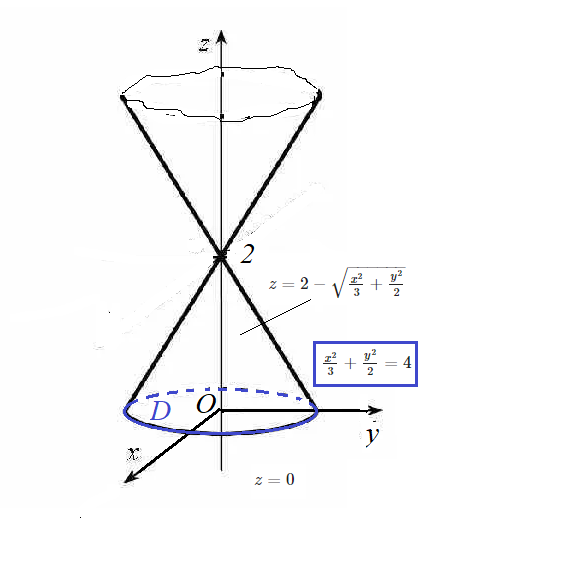
[m]z-2=-\sqrt{\frac{x^2}{3}+\frac{y^2}{2}}[/m] ⇒ [m]z=2-\sqrt{\frac{x^2}{3}+\frac{y^2}{2}}[/m]
[m]V= ∫ ∫_{D}(2-\sqrt{\frac{x^2}{3}+\frac{y^2}{2}})dxdy=[/m]
D:
область ограниченная, линией пересечения плоскостей:
[m]z=2-\sqrt{\frac{x^2}{3}+\frac{y^2}{2}}[/m] и [m]z=0[/m]
[m]2-\sqrt{\frac{x^2}{3}+\frac{y^2}{2}}=0[/m]
[m]\sqrt{\frac{x^2}{3}+\frac{y^2}{2}}=2[/m]
[m]\frac{x^2}{3}+\frac{y^2}{2}=4[/m]
Делим на 4:
[m]\frac{x^2}{12}+\frac{y^2}{8}=1[/m] - каноническое уравнение эллипса
[m]a^2=12; b^2=8[/m]
Переход к обобщенным полярным координатам :
[m]x=arcos φ=\sqrt{12}rcos φ [/m]
[m]y=brsin φ=\sqrt{8}rsin φ [/m]
[m]dxdy=abrdrd φ=\sqrt{96}rdrd φ=4\sqrt{6}rdrd φ [/m]
[m]= ∫^{2π}_{0} (∫^{1}_{0}(2-\sqrt{\frac{(\sqrt{12}rcos φ )^2}{3}+\frac{(\sqrt{8}rsin φ)^2 }{2})}4\sqrt{6}rdr)d φ =[/m]
[m]=4\sqrt{6}∫^{2π}_{0} (∫^{1}_{0}(2-\sqrt{4r^2cos^2 φ +4r^2sin^2 φ )}rdr)d φ =4\sqrt{6}∫^{2π}_{0} (∫^{1}_{0}(2-\sqrt{4r^2(cos^2 φ +sin^2 φ )}rdr)d φ =[/m]
[m]=4\sqrt{6}∫^{2π}_{0} (∫^{1}_{0}(2-2\sqrt{r^2})rdr)d φ =4\sqrt{6}∫^{2π}_{0} (∫^{1}_{0}(2-2r)rdr)d φ =8\sqrt{6}∫^{2π}_{0} (∫^{1}_{0}(r-r^2)dr)d φ=[/m]
[m]=8\sqrt{6}∫^{2π}_{0}(\frac{r^2}{2}-\frac{r^3}{3})|^{1}_{0})d φ =8\sqrt{6}∫^{2π}_{0}(\frac{1^2}{2}-\frac{1^3}{3}))d φ=8\sqrt{6}∫^{2π}_{0}(\frac{1}{6})d φ=\frac{8}{6}\sqrt{6}( φ )|^{2π}_{0}=\frac{8\sqrt{6}π}{3}[/m]
3.
Через тройной интеграл:
[m] V= ∫ ∫ ∫_{ Ω }dxdydz[/m]
⇒
[m] V= ∫ ∫ _{D }( ∫^{2-\sqrt{\frac{x^2}{3}+\frac{y^2}{2}}}_{0}dz)dxdy[/m]= далее все как в двойном интеграле