Задача 54858 Используя лишь определение предела,...
Условие
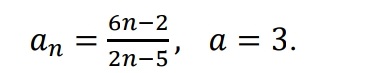
Решение
[m]|a_{n}–a| = |\frac{6n-2}{2n-5}–3| = |\frac{6n-2-3\cdot (2n-5)}{2n-5}|=|\frac{6n-2-
6n+15)}{2n-5}|=|\frac{13)}{2n-5}|=\frac{13}{2n-5}[/m]
В определении эта разность должна быть меньше некоторого положительного числа [m] ε[/m]
[m]|a_{n}–a| < ε[/m]
Решаем неравенство
[m]\frac{13}{2n-5} < ε[/m] ⇒
[m] \frac{2n-5}{13} >\frac{1}{ε}[/m] ⇒
[m]2n-5 > \frac{13}{ε}[/m] ⇒
[m]2n >5+ \frac{13}{ε}[/m] ⇒
[m]n > \frac{5+ \frac{13}{ε}}{2}[/m]
Для любого [m] > 0 [/m] найдется [m] N( ε)= [\frac{5+ \frac{13}{ε}}{2}]+1[/m], - целой части числа [m]\frac{5+ \frac{13}{ε}}{2}[/m] плюс 1 ( с запасом), что для всех [m] n > N( ε)[/m]
выполняется [m] |\frac{6n-2}{2n-5}–3| < ε[/m]
что и означает, что предел последовательности [m] (\frac{6n-2}{2n-5})[/m] равен 3