Задача 54857 Методом математической индукции...
Условие
некоторого номера 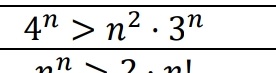
Решение
n_(o) - ищите, начиная с какого n это неравенство верно
Предположение:
[m] 4^{n} > n^2\cdot 3^{n}[/m] - верно
Доказать
[m] 4^{n+1} > (n+1)^2\cdot 3^{n+1}[/m] - верно
Доказательство
[m] 4^{n+1} =4\cdot 4^{n} [/m] используем предположение > [m] 4 \cdot n^2\cdot 3^{n}=[/m]
[m] =(3+1) \cdot n^2 \cdot 3^{n}=n^2\cdot 3^{n+1}+n^2\cdot 3^{n}=[/m]
выделяем то, что требуется получить в правой части и вычитаем то что прибавили:
[m] (n+1)^2\cdot 3^{n+1}+n^2\cdot 3^{n}-2n\cdot 3^{n+1}-3^{n+1}=(n+1)^2\cdot 3^{n+1}+3^{n}\cdot (n^2-6n-3)[/m]
мне не нравится, потому что cправа сумма двух слагаемых. Сумма всегда больше. А верно будет только в том случае, если второе слагаемое с минусом, т.е
[m]n^2-6n-3 <0[/m]
при 2-2sqrt(3) n<3+2sqrt(2)= 5,...
Значит верно, только для [b]n=1,2,3,4,5[/b]
но проверка показывает, что
[m] 4^{5} > 5^2\cdot 3^{5}[/m] - неверно
Поэтому может опечатка в условии???