Задача 54254 Вычислите пределы числовых...
Условие

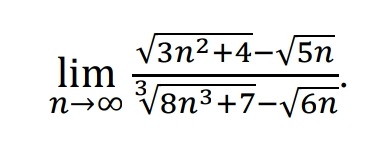
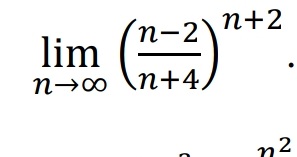
Решение
[m]\lim_{ n \to \infty }(n+\sqrt[3]{4-n^3})=[/m]Неопределенность ( ∞ - ∞ )
Умножаем и делим на
[m](n^2-n\cdot \sqrt[3]{4-n^3}+\sqrt{(4-n^3)^2})[/m]
в числителе формула cуммы кубов [b](a+∛b)*(a^2-a∛b+∛b^2)=a^3+b[/b]
[m]=\lim_{ n \to \infty }\frac{n^3+(4-n^3)}{n^2+n\cdot \sqrt[3]{4-n^3}-\sqrt{(4-n^3)^2}}=[/m]
Раскрываем скобки в числителе:
[m]=\lim_{ n \to \infty }\frac{4}{n^2+n\cdot \sqrt[3]{4-n^3}-\sqrt{(4-n^3)^2}}=0[/m]
2)Неопределенность ( ∞ - ∞ )/( ∞ - ∞ )
Делим числитель и знаменатель на n в высшей степени, т. е на n:
[m]=\lim_{ n \to \infty }\frac{\frac{\sqrt{3n^2+4}-\sqrt{5n}}{n}}{\frac{\sqrt[3]{8n^3+7}-\sqrt{6n}}{n}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на n и
каждое слагаемое знаменателя делим на n
[m]\lim_{ n \to \infty }\frac{\frac{\sqrt{3n^2+4}}{n}-\frac{\sqrt{5n}}{n}}{\frac{\sqrt[3]{8n^3+7}}{n}-\frac{\sqrt{6n}}{n}}[/m]
Применяем свойства корня:
[m]\lim_{\to \infty }\frac{\sqrt{\frac{3n^2+4}{n^2}}-\sqrt[3]{\frac{5n}{n^2}}}{\sqrt[7]{\frac{8n^3+7}{n^3}-\sqrt\frac{6n}{n^2}}}=[/m]
[m]=\frac{\sqrt{3}-0}{\sqrt[3]{8}-0}=\frac{\sqrt{3}}{2}[/m]
3)
[m]=\lim_{ n \to \infty }(\frac{n-2}{n+4})^{n+2}=[/m]
по свойству степени:
[m]=\lim_{ n \to \infty }(\frac{n-2}{n+4})^{n}\cdot\lim_{ n \to \infty }(\frac{n-2}{n+4})^{2}=\lim_{ n \to \infty }(\frac{n-2}{n+4})^{n}\cdot 1 [/m] ( неопределенность 1^( ∞ ) )
Делим числитель и знаменатель дроби [m] \frac{n-2}{n+4} [/m] на n
[m]=\lim_{ n \to \infty }(\frac{\frac{n-2}{n}}{\frac{n+4}{n}})^{n}=\lim_{ n \to \infty }(\frac{(1-\frac{2}{n})^{n}}{(1+\frac{4}{n})^{n}}=[/m]
Применяем второй замечательный предел: [m]\lim_{ n \to \infty }(1+\frac{1}{n})^{n}=e[/m] и [m]\lim_{ n \to \infty }(1+\frac{k}{n})^{n}=e^{k}[/m]
[m]=\frac{e^{-2}}{e^{4}}=e^{-6}[/m]