Задача 53798 ...
Условие
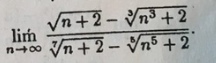
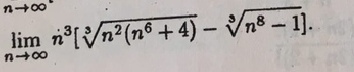
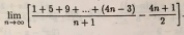
Решение
Делим и числитель и знаменатель на n
[m]=\lim_{ n \to \infty }\frac{\frac{\sqrt{n+2}-\sqrt[3]{n^3+2}}{n}}{\frac{\sqrt[7]{n+2}-\sqrt[5]{n^5+2}}{n}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на n и
каждое слагаемое знаменателя делим на n
[m]\lim_{ n \to \infty }\frac{\frac{\sqrt{n+2}}{n}-\frac{\sqrt[3]{n^3+2}}{n}}{\frac{\sqrt[7]{n+2}}{n}-\frac{\sqrt[5]{n^5+2}}{n}}[/m]
Применяем свойства корня:
[m]\lim_{\to \infty }\frac{\sqrt{\frac{n+2}{n^2}}-\sqrt[3]{\frac{n^3+2}{n^3}}}{\sqrt[7]{\frac{n+2}{n^7}-\sqrt[5]\frac{n^5+2}{n^5}}}=[/m]
[m]=\frac{\sqrt{0}-1}{\sqrt[7]{0}-1}=1[/m]
2) Неопределенность ( ∞ - ∞ )
Умножаем и делим на [m]\sqrt[3]{n^2\cdot (n^6+4)^2}+\sqrt[3]{n^2\cdot (n^6+4)}\cdot \sqrt[3]{n^8-1}+(\sqrt[3]{n^8-1})^2[/m]
В числителе - формула [m](\sqrt[3]{a}-\sqrt[3]{b})\cdot ((\sqrt[3]{a})^2+\sqrt[3]{a}\cdot \sqrt[3]{b}+(\sqrt[3]{b})^2)=a-b[/m]
[m]=\lim_{ n \to \infty }\frac{n^3\cdot (n^2\cdot (n^6+4)-(n^8-1))}{(\sqrt[3]{n^2\cdot (n^6+4))^2}+\sqrt[3]{n^2\cdot (n^6+4)}\cdot (\sqrt[3]{n^8-1})+(\sqrt[3]{n^8-1})^2}=[/m]
Раскрываем скобки в числителе:
[m]=\lim_{ n \to \infty }\frac{n^3\cdot (4n^2+1)}{(\sqrt[3]{n^2\cdot (n^6+4))^2}+\sqrt[3]{n^2\cdot (n^6+4)}\cdot (\sqrt[3]{n^8-1})+(\sqrt[3]{n^8-1})^2}=[/m]
Делим на n в высшей степени ( это[m] (n^{\frac{8}{3}})^2[/m])
[m]=\frac{0}{1+1+1}=0[/m]
3)
По формуле суммы арифметической прогрессии
[m]1+5+9+...+(4n-3)=\frac{(1+4n-3)\cdot n}{2}=(2n-1)\cdot n=2n^2-n[/m]
Тогда
[m]=\lim_{ n \to \infty }(\frac{2n^2-n}{n+1}-\frac{4n+1}{2})=\lim_{ n \to \infty }\frac{-7n-1}{2(n+1)}=-3,5[/m]