Задача 4581 Найти наибольшее значение выражения...
Условие
математика 10-11 класс
4790
Решение
★
–6x2·y2+x3·y–c=0
6x2·y2–x3·y+c=0 я знаки поменял
посчитаем дискриминант.
D=x6–24x2·c>=0
поделим на x2
x4–24c>=0 выразим с
24с<=x4 х макс=3
с макс=81/24=3.375
Обсуждения
Все решения
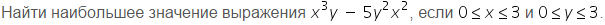

Обсуждения
Обсуждения
