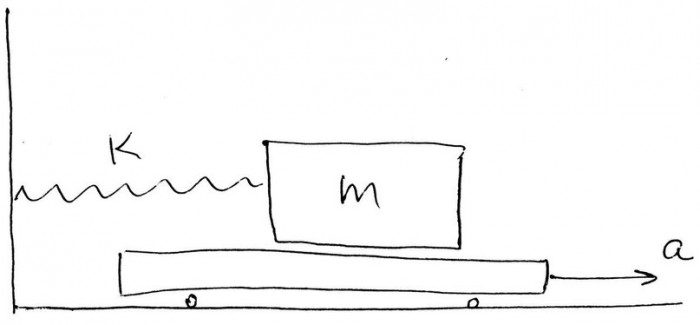
Ответ t=sqrt(2m1(mg-a)/ka) выглядит странно. Если взять a равным mg, то время получится нулевым, если бОльшим, чем mg, то вообще под корнем отрицательная величина получится.
Также не ясно, как учитывается тот факт, что сначала мы имеем дело с силой трения покоя, которая меньше силы трения скольжения.