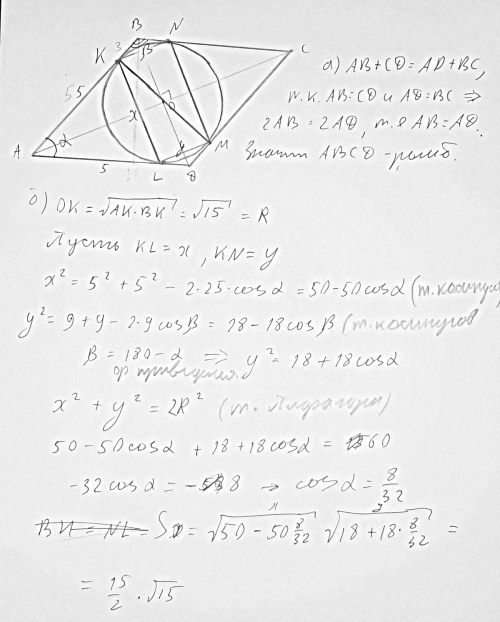Условие
В параллелограмм вписана окружность.
а) Докажите, что этот параллелограмм - ромб.
б) Окружность, касающаяся стороны ромба, делит её на отрезки, равные 5 и 3. Найдите площадь четырёхугольника с вершинами в точках касания окружности со сторонами ромба.
математика 10-11 класс
26799
Решение
KL и MN находим по теореме косинусов. Так как бета + альфа = 180, можно выразить альфа через бета и подставить в косинус, по формуле приведения (cos(180-a) = -cosa) косинус станет отрицательным. Теперь можно составить уравнением исходя из того, что KL^2 + KN^2 = KM^2 это следует из теоремы Пифагора. Только учтите, что KM = 2OK = 2R. Решив уравнение, находим косинус альфа и соответственно 2 стороны (x и y) прямоугольника. Далее площадь S = xy
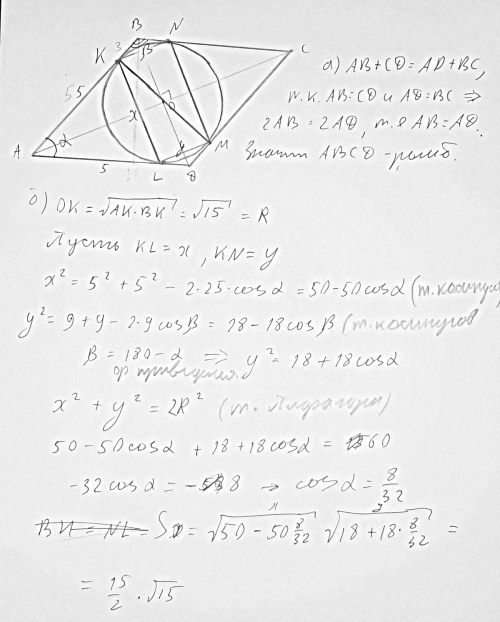
Ответ: 15*sqrt(15)/2
Вопросы к решению (3)
почему КNML прямоугольник?
Логически так, другой фигуры быть не может
Почему knml не может быть квадратом?
при нахождении cos альфа ошибка должно получиться 68 - 32 cos альфа = 2,125
Все решения
В окружности будет прямоугольник, так как из подобия треугольников понятно, что диагонали ромба будут параллельны сторонам четырехугольника...)
А диагонали ромба пересекаются под прямым углом...))
Написать комментарий