Задача 12762 Решить: (13-9^(-x))/(4-3^(-x))=12...
Условие
Отобрать корни: [-2;-3/2]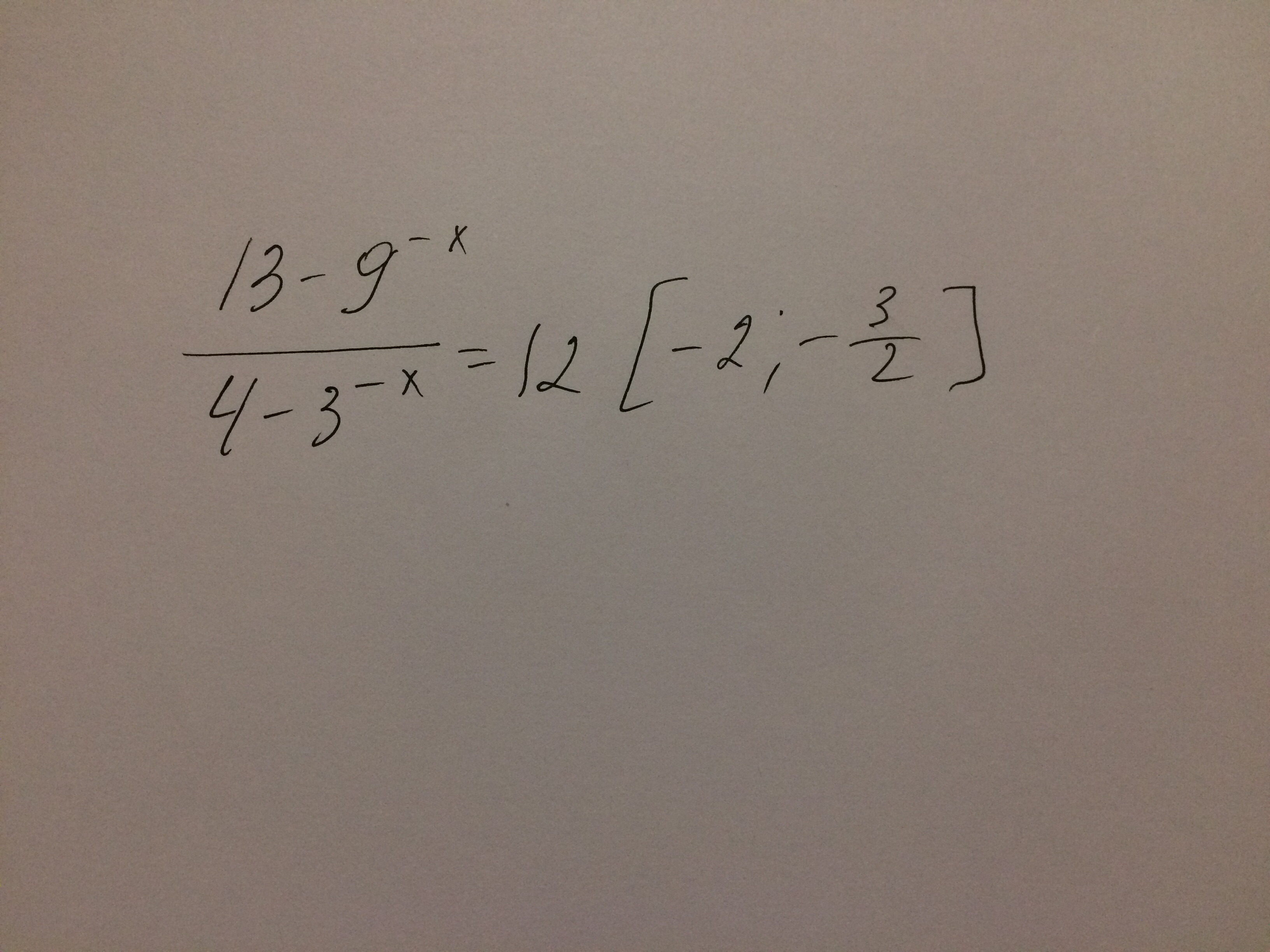
Решение
3^(-х)=t; t > 0
9^(-x)=t^2
(13-t^2)/(4-t)=12;
13-t^2=48-12t;
t^2-12t+35=0
D=144-140=4
t=5 или t=7
3^(-x)=5 или 3^(-х)=7
-x=log_(3)5 или -х= log_(3)7
log_(3)9=2; log_(3)(3sqrt(3))=3/2
Логарифмическая функция с основанием 3 возрастающая, поэтому
так как 9 > 7 > 3sqrt(3) > 5, то
log_(3)9 > log_(3)7 > log_(3)(3sqrt(3)) > log_(3)5
или что то же самое:
log_(3)5 < log_(3)(3sqrt(3)) < log_(3)7 < log_(3)9
Умножаем на (-1), знак неравенства изменится на противоположный.
-log_(3)5 > -log_(3)(3sqrt(3)) > -log_(3)7 > -log_(3)9
или что то же самое
-log_(3)9 < -log_(3)7 < -log_(3)(3sqrt(3)) < -log_(3)5
-2 < - log_(3)7 < -3/2
б) о т в е т. - log_(3)7=log_(3)(1/7)∈[-2;-3/2]