Задача 10289 ...
Условие
Решение
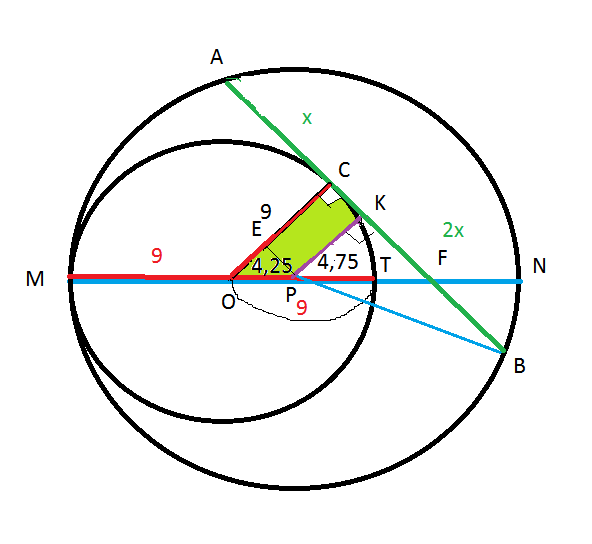
Пусть хорда АВ окружности радиуса 13,25 касается окружности радиуса 9 в точке С.
См. рисунок.
ОС=ОМ=ОТ=9 - радиус меньшей окружности.
РМ=PN=PB=13,25 - радиус большей окружности.
РО=РМ-ОМ=13,25-9=4,25
Проведем РК⊥АВ.
РК- часть диаметра окружности радиуса 13,25.
Диаметр, перпендикулярный хорде делит эту хорду пополам.
Пусть АС=х, ВС=2х. По условию АС:ВС=х:2х=1:2.
АВ=АС+СВ=х+2х=3х.
Значит АК=КВ=1,5х;
СК=АК-АС=1,5х-х=0,5х.
Из прямоугольного треугольника РКВ:
РК^2=PB^2-KB^2
PK^2=(13,25)^2-(1,5x)^2
Рассмотрим прямоугольную трапецию ОСКР.
Проведем высоту РЕ.
Из прямоугольного треугольника ОЕР:
ОЕ^2+PE^2=OP^2
РЕ=КС=0,5х
EC=PK=√((13,25)^2-(1,5x)^2)
ОЕ=9-√((13,25)^2-(1,5x)^2)
(9-√((13,25)^2-(1,5x)^2))^2 +(0,5х)^2=(4,25)^2;
81-18√((13,25)^2-(1,5x)^2)+(13,25)^2-(1,5x)^2+0,25x^2=(4,25)^2.
или
18√((13,25)^2-(1,5x)^2)=81+(13,25)^2-(4,25)^2-2x^2;
18√((13,25)^2-(1,5x)^2)=81+17,5•9-2x^2;
18√((13,25)^2-(1,5x)^2)=9•26,5-2x^2.
Возводим в квадрат:
4х^4-225x^2=0
x^2(4x^2-225)=0
x^2=225/4;
x=15/2=7,5.
AB=3x=22,5.
О т в е т. АВ=22,5.