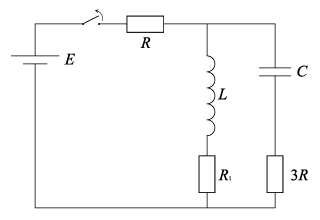
В цепи, схема которой показана на рисунке, ключ замкнут, режим установился. Какое количество теплоты выделится в цепи после размыкания ключа? R = 10 Ом, R1 = 2R, L = 2 мГн, С = 20 мкФ, E = 12 В. Внутренним сопротивлением источника пренебречь.
физика 10-11 класс
10741
1. в уст режиме через кондер тока нет, а катушка= проводу, ток в катушке по закону ома I=E/2R=0.6А. Напряжение на кондере=E/2, тк оно равно напряжению на втором резисторе (тк они подключены к одинаковым узлам) а известно что в последовательной цепи напряжение делится на резисторах поровну.
2. После выкл. будет выделяться теплота только на резисторах, но нам не важно как, главное что вся энергия перейдет в тепло (по закону о сохранении энергии). Вот и получится что выделится то, что накопилось на кондере и в катушке. то есть
Q=cU^2/2 +LI^2/2=1,8мДж
Вопросы к решению (1)
Напряжение на кондере=E/2, тк оно равно напряжению на втором резисторе (тк они подключены к одинаковым узлам) а известно что в последовательной цепи напряжение делится на резисторах поровну. в задаче же нет резисторов с один. сопротивлением, чтобы делить поровну?
ток идет через левую ветку, и напряжение на кондере будет как на левом резисторе.
