Векторная алгебра Часть I

Понятие вектора. Проекции вектора.

Линейные операции над векторами.

Понятие вектора. Проекции вектора

Направленные отрезки принято называть также геометрическими векторами или просто векторами. Вектор как направленный отрезок мы будем по-прежнему записывать в тексте двумя большими латинскими буквами с общей чертой наверху при условии, что первая из них обозначает начало, вторая - конец вектора. Наряду с этим мы будем также обозначать вектор одной малой латинской буквой полужирного шрифта, которая на чертежах ставится у конца стрелки, изображающей вектор (рис. 1, где изображен вектор а с началом А и концом В). Начало вектора часто будет называться также его точкой приложения.

Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.

Число, равное длине вектора (при заданном масштабе), называется его модулем. Модуль вектора a обозначается символом |vector{a}| или а. Если |vector{a}|=1, то вектор vector{a} называется единичным.

Единичный вектор, имеющий одинаковое направление с данным вектором vector{a}, называется ортом вектора vector{a} и обозначается обычно символом a^(-0).

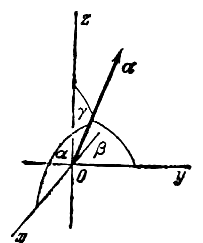
Проекцией вектора vector{AB} на ось u называется число, равное величине отрезка A1B1 оси u, где точка A1 является проекцией точки А на ось u, а B1 - проекцией точки В на эту ось.

Проекция вектора vector{AB} на ось u обозначается символом пр_uvector{AB}.

Проекция вектора vector{a} на ось u выражается через его модуль и угол phi наклона к оси u формулой

пр_uvector{a} = |vector{a}|*cosphi

Проекции произвольного вектора vector{a} на оси некоторой заданной системы координат в дальнейшем обозначаются буквами X, Y, Z. Равенство vector{a}={X, Y, Z} означает, что числа X, Y, Z являются проекциями вектора на координатные оси. Вектор, для которого X=Y=Z=0, называется нулевым и обозначается vector{0}.

Проекции вектора на координатные оси называются также его (декартовыми) координатами. Если даны две точки M1(x1, y1, z1) и M2(x2, y2, z2), являющиеся соответственно началом и концом вектора vector{a}, то его координаты X, Y, Z определяются по формулам X=x1-x2, Y=y2-y1, Z=z2-z1.

Формула

vector{a} = sqrt(X^2 + Y^2 + Z^2) (2)

позволяет по координатам вектора определить его модуль.

Если альфа, бета, гамма - углы, которые составляет вектор vector{a} с координатными осями (см. рис. 2), то cosальфа, cosбета, cosгамма называются направляющими косинусами вектора vector{a}.

Вследствие формулы (1)

X = |vector{a}|cosальфа, Y = |vector{a}|cosбета, Z = |vector{a}|cosгамма .

Отсюда, и из формулы (2) следует, что

cos^2альфа + cos^2бета + cos^2гамма = 1.

Последнее равенство позволяет определить один из углов альфа, бета, гамма , если известны два других.

ЗАДАЧА 3724 Даны точки A(3; -1; 2), B(-1; 2; 1).

Даны точки A(3; -1; 2), B(-1; 2; 1). Найти координаты векторов vector{AB} и vector{BA}. Смотреть решение...

Линейные операции над векторами

Суммой vector{a}+vector{b} двух векторов vector{a} и vector{b} называется вектор, который идет из начала вектора vector{a} в конец вектора vector{b} при условии, что вектор vector{b} приложен к концу вектора vector{a} (правильно треугольника). Построение суммы vector{a}+vector{b} изображено на рис. 1.

Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы vector{a} и vector{b} приведены к общему началу и на них построен параллелограмм, то сумма vector{a}+vector{b} есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала vector{a} и vector{b} (рис. 2). Отсюда сразу следует, что vector{a}+vector{b} = vector{b}+vector{a}.

Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов vector{a}, vector{b} , vector{c} , vector{d} ).

Разность vector{a}-vector{b} двух векторов vector{a} и vector{b} называется вектор, который в сумме с вектором vector{b} составляет вектор vector{a}. Если два вектора vector{a} и vector{b} приведены к общему началу, то разность их vector{a}-vector{b} есть вектор, идущий из конца vector{b} («вычитаемого») к концу vector{a} («уменьшаемого»). Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом vector{a}, то другой обозначается символом -vector{a}. Легко видеть, что vector{a}-vector{b} = vector{a}+(-vector{b}). Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».

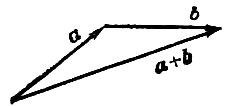
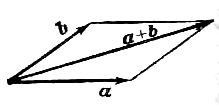
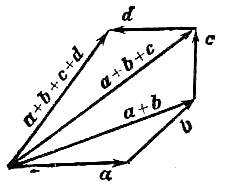
Произведение альфаvector{a} вектора vector{a} на число альфа называется вектор, модуль которого равен произведению модуля вектора vector{a} на модуль числа альфа; он параллелен вектору vector{a} или лежит с ним на одной прямой и направлен так же, как вектор vector{a} , если альфа - число положительное, и противоположно вектору vector{a} , если альфа - число отрицательное.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

Имеют место следующие две основные теоремы о проекциях векторов:

1) Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось.

2) При умножении вектора на число его проекция умножается на то же число.

В частности, если

vector{a} = (X1; Y1; Z1), vector{b} = (X2; Y2; Z2)

то

vector{a} + vector{b} = {X1+X2; Y1+Y2; Z1+Z2}

vector{a} - vector{b} = {X1-X2; Y1-Y2; Z1-Z2}

Если vector{a} = {X; Y; Z}, то для любого числа альфа

альфаvector{a} = {альфаX; альфаY; альфаZ}

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов

vector{a} = (X1; Y1; Z1), vector{b} = (X2; Y2; Z2)

является пропорциональность их координат:

X2/X1 = Y2/Y1 = Z2/Z1

Тройка векторов vector{i}, vector{j}, vector{k} называется координатным базисом, если эти векторы удовлетворяют следующим условиям:

1). Вектор vector{i} лежит на оси Ох, вектор vector{j} - на оси Оу, вектор vector{k} - на оси Oz;

2). Каждый из векторов vector{i}, vector{j}, vector{k} направлен по своей оси в положительную сторону;

3). Векторы vector{i}, vector{j}, vector{k} единичные, то есть vector{i}=1, vector{j}=1, vector{k} =1 .

Каким бы ни был вектор vector{a}, он всегда может быть разложен по базису vector{i}, vector{j}, vector{k} , то есть может быть представлен в виде

vector{a} = Xvector{i} + Yvector{j} + Zvector{k}

коэффициенты этого разложения являются координатами вектора vector{a}(то есть X, Y, Z суть проекции вектора vector{a} на координатные оси).

ЗАДАЧА 3725 Векторы vector{a} и vector{b} образуют

Векторы vector{a} и vector{b} образуют угол phi=1200, причем |vector{a}|=3 и |vector{b}|=5. Определить |vector{a} + vector{b}| и |vector{a} - vector{b}|. Смотреть решение...