Максимум и минимум функции. Наибольшее и наименьшее значение функции.
Правило отыскания наибольшего и наименьшего значений функции: чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Критические точки: – внутренние точки области, в которых ее производная равна нулю или не существует.
Правила вычисления производных:
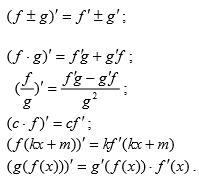
Таблица производных:
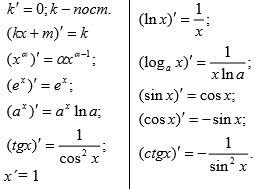
Применяя изложенный выше метод поиска наибольшего и наименьшего значений функции, будем следовать алгоритму:
Найти наименьшее значение функции y=(x^2-7x+7)e^(x-5) на отрезке [4; 6].
Смотреть решение...
Признак максимума и минимума функции: если в точке х0 производная меняет знак с «+» на «-», то х0 есть точка максимума, с «-» на «+», то х0 – точка минимума.
При решении практических задач на нахождение точки максимума или минимума функции следуем такому алгоритму:
Найдите точку максимума функции y=t^3/3 2t^2-5t-2.
Смотреть решение...
Критические точки: – внутренние точки области, в которых ее производная равна нулю или не существует.
Правила вычисления производных:
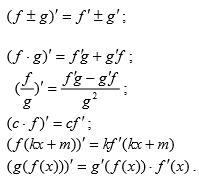
Таблица производных:
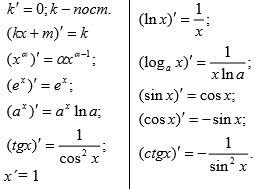
Применяя изложенный выше метод поиска наибольшего и наименьшего значений функции, будем следовать алгоритму:
- 1) найдем производную данной функции;
- 2) приравняем ее к нулю;
- 3) выберем критические точки, лежащие внутри отрезка;
- 4) найдем значение функции в этих точках и на концах отрезка;
- 5) из полученных чисел выберем наибольшее или наименьшее.
ЗАДАЧА 1578 Найти наименьшее значение функции
Найти наименьшее значение функции y=(x^2-7x+7)e^(x-5) на отрезке [4; 6].
Смотреть решение...
Признак максимума и минимума функции: если в точке х0 производная меняет знак с «+» на «-», то х0 есть точка максимума, с «-» на «+», то х0 – точка минимума.
При решении практических задач на нахождение точки максимума или минимума функции следуем такому алгоритму:
- 1) найдем область определения данной функции;
- 2) найдем производную данной функции;
- 3) приравняем ее к нулю;
- 4) найдем промежутки знакопостоянства функции;
- 5) найдем точку максимума или минимума.
ЗАДАЧА 1579 Найдите точку максимума функции
Найдите точку максимума функции y=t^3/3 2t^2-5t-2.
Смотреть решение...
Просмотры: 6821 |
Статью добавил: slava191 |
Категория: математика
☰ Меню