Задача 8941 Одна ячейка памяти (один трит) троичной...
Условие
информатика 10-11 класс
3405
Решение
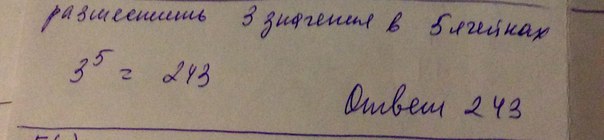
Ответ: 243
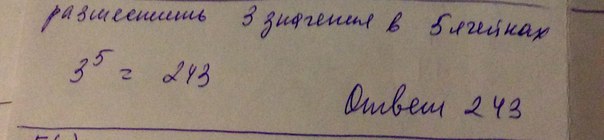
Ответ: 243