Задача 8537 ...

Mari 13

16.04.2016

Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.

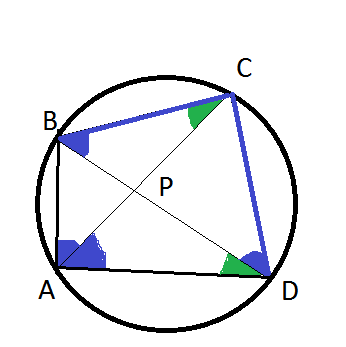
а) Докажите, что AB:BC=AP:PD.

б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB=5, а BC=5√2

SOVA

16.04.2016

★

а)СD= BC. Равные хорды стягивают равные дуги.
Значит дуга ВС равна дуге CD.
Вписанный угол измеряется половиной дуги, на которую он опирается.
Поэтому углы, опирающиеся на дуги BC и CD равны.
Отмечены синим цветом.
Углы, опирающиеся на дугу АВ, также равны (отмечены зеленым).
Треугольники АВС и APD подобны по двум углам.
Из подобия:
АВ:ВС=АР:РD.

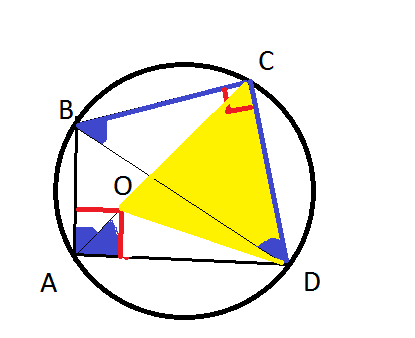
б)BD- диаметр, угол, опирающийся на диаметр равен 90°.
Треугольник ВСD- прямоугольный равнобедренный.
BD=5√2/sin 45°=10.
В прямоугольном треугольнике ABD катет АВ=5, гипотенузы BD=10. Катет против угла в 30° равен половине гипотенузы. Значит ∠ АDВ=30°.
∠ АВD=60°.
∠ АСD=∠ АВD=60° как углы опирающиеся на одну дугу AD.

Центр окружности, вписанной в треугольник ABD- точка пересечения биссектрис.

АС- биссектриса ∠ ВАD.
OD- биссектриса ∠ АDВ.

∠ ODC=∠ ODB+∠ BDC=15°+45°=60°.

Треугольник OCD- равносторонний.

∠ АСD=60°;∠ ODC=∠ ODB+∠ BDC=15°+45°=60°, значит и третий угол 60°.

S (Δ OCD)=CD²•√3/4=25•√3/2 кв. ед.