Задача 8330 ...

slava191

03.04.2016

Окружности ω1 и ω2 касаются внешним образом. A1A2 и B1B2 - их общие внешние касательные (A1 и B1 - точки касания ω1, A2 и B2 - точки касания с ω2).

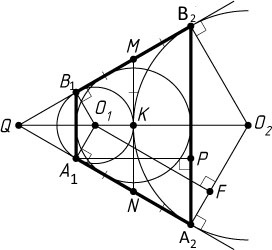
А) Докажите, что расстояние между хордами A1B1 и A2B2 равно среднему гармоническому диаметров окружностей. (средним гармоническим двух положительных чисел а и b называется значение выражения 2/(1/a + 1/b))

Б) Найдите площадь четырехугольника A1A2B2B1, если радиусы окружностей равны соответственно 9 и 4.

Julia_Trusova

05.04.2016

★

А)Пусть r-радиус первой окружности, R-радиус второй окружности. Р-проекция А1 на А2В2, то есть А1Р-расстояние от A1A2 до B1B2
Требуется доказать, что А1Р=2/(1/(2r) + 1/(2R)))=2/((R+r)/(2Rr))=(4rR)/(R+r)
A1A2∩ B1B2=Q
ΔA1QB1 и ΔA2QB2-равнобедренные
=>A1B1||A2B2,
=>A2A1B1B2-равнобедренная трапеция
Так как в равнобедренную трапецию можно вписать окружность, то диаметр этой окружности и будет равен расстоянию от A1A2 до B1B2
А1Р-высота трапеции, А1Р=диаметру окружности, вписанной в трапецию .
Пусть F — проекция точки O1 на O2А2.
О1О2=R+r, O2F=R-r,
Из ΔО1О2F по теореме Пифагора: О1F=2sqrt(rR)
Δ А1РА2~ΔО1FО2 (по двум углам)
=>А1Р=А1А2*О1F/O1O2
A1A2=O1F
А1Р=2sqrt(rR)* 2sqrt(rR)/(R+r)= (4rR)/(R+r)
Что и требовалось доказать.

Б)r=4, R=9
S(A2A1B1B2)=A1P*MN
MN-средняя линия, K-точка касания окружностей(MK = KN, AN = NK = ND-по свойству касательных, BM = MK = MC-по свойству касательных.)
MN=A1A2=O1F=2sqrt(4*9)=12
A1P=4*4*9/(9+4)=144/13
S(A2A1B1B2)= 144/13*12=1728/13
Ответ:1728/13