Задача 7994 Все ребра правильной четырехугольной...

slava191

22.03.2016

Все ребра правильной четырехугольной пирамиды FABCD с основанием ABCD равны 7. Точки P,Q,R лежат на ребрах FA, AB и ВС соответственно, причем FP=BR=4, AQ=3.

А) Докажите, что плоскость PQR перпендикулярна ребру FD
Б) Найдите расстояние от вершины D до плоскости PQR

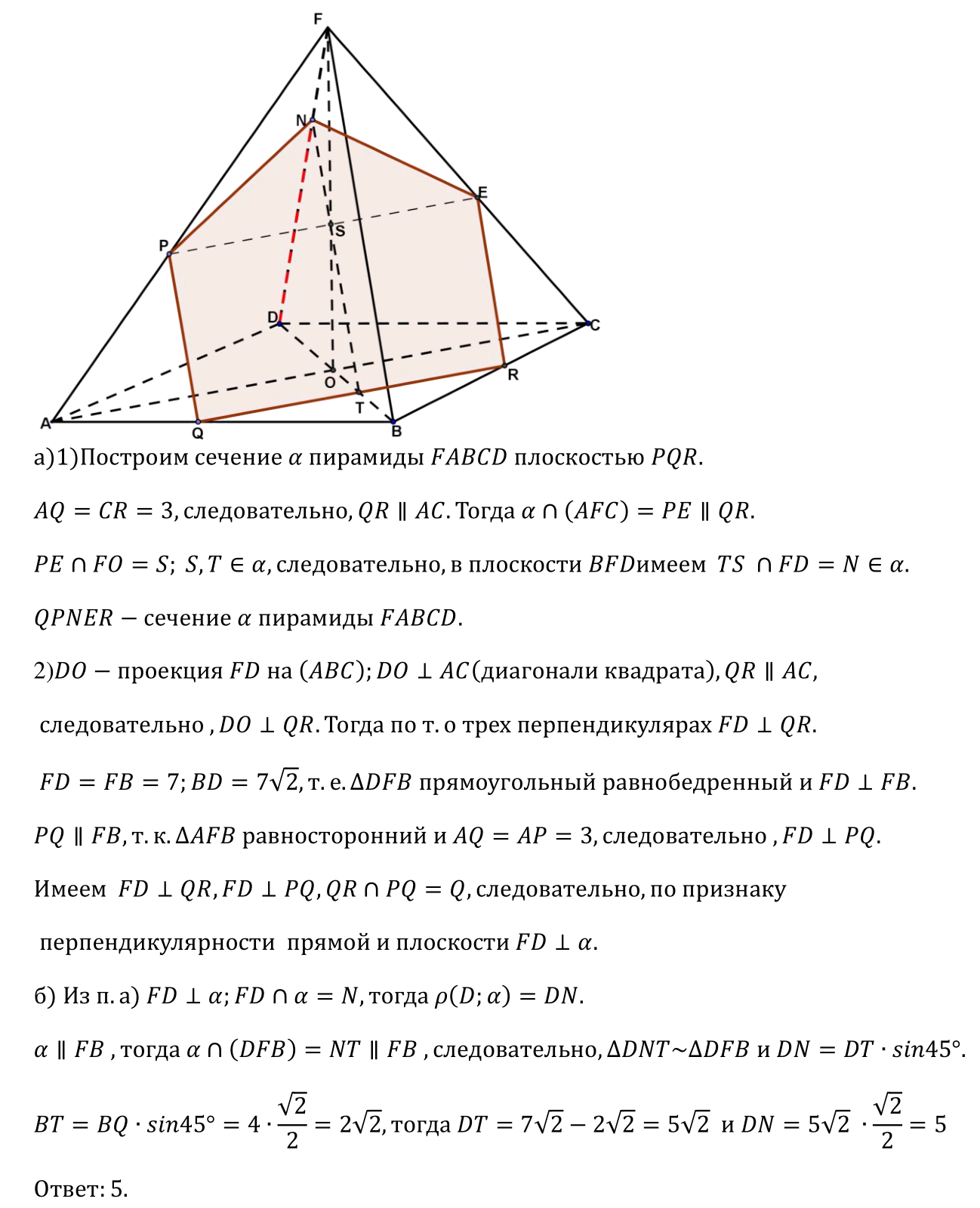
Ответ: 5