Задача 7481 Значения двух массивов А и В с индексами...
Условие
Какое количество элементов массива В[1..100] будет принимать положительные значения после выполнения данной программы?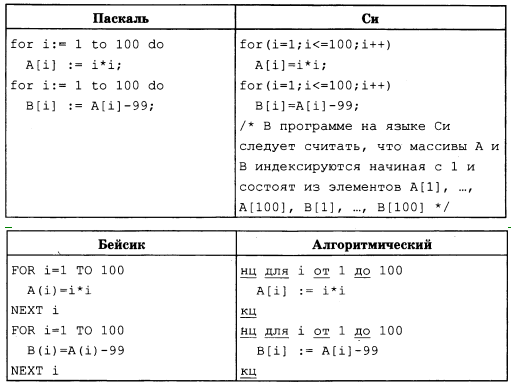
Решение
В первом цикле, в массиве A, квадраты чисел от 1 до 100, то есть: 1, 4, 9, 16 и тд.
Во втором цикле, в массиве B, из чисел, которые получились в массиве А, вычитается число 99.
Нам нужно количество положительных чисел, которые получились в массиве B. Но для этого не надо считать весь массив. Достаточно посчитать первые десять чисел:
1 - 99 (отрицательное)
4 - 99 (отрицательное)
9 - 99 (отрицательное)
16 - 99 (отрицательное)
25 - 99 (отрицательное)
36 - 99 (отрицательное)
49 - 99 (отрицательное)
64 - 99 (отрицательное)
81 - 99 (отрицательное)
100 - 99 (положительное)
Остальные числа будут ещё больше, а следовательно, положительные.
Итого, в массиве было 100 чисел, 9 отрицательных, значит положительных 91. Вот и ответ.
Ответ: 91
