Задача 6809 В сосуде, закрытом поршнем, находится...

anderzhanov.din

14.02.2016

В сосуде, закрытом поршнем, находится идеальный газ. На рисунке показана зависимость давления газа от температуры при изменении его состояния. Как меняется объем газа при переходе из В в С?

1) увеличивается
2) уменьшается
3) не изменяется
4) по данной зависимости нельзя определить изменение объема газа

Идеальный газ подчиняется уравнению Клапейрона-Менделеева: pV = nRT.

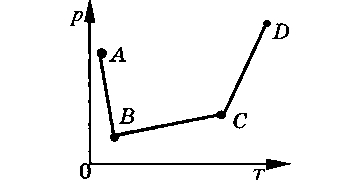
V = nRT/p. При переходе из B в C давление увеличивается (что свидетельствует о сжатии), но температура повышается (что свидетельствует о расширении)

Ответ: 4