Задача 4780 Ученые опросили группу 45-летних жителей...
Условие
Какие выводы можно сделать из полученных результатов? Выберите из списка нужные позиции и запишите цифры, под которыми они указаны.
1) Мужчины и женщины единодушны в определении главного фактора, снижающего воспитательный потенциал семьи.
2) Мужчины в большей степени, чем женщины, ощущают нехватку знаний, необходимых для воспитания детей.
3) Плохие отношения между родителями как причина снижения воспитательного потенциала семьи недооцениваются опрошенными.
4) Женщины более негативно оценивают вмешательство родственников в воспитание детей, чем мужчины.
5) При оценке различных факторов, влияющих на воспитание детей, мужчины в меньшей степени, чем женщины, придают значение составу семьи.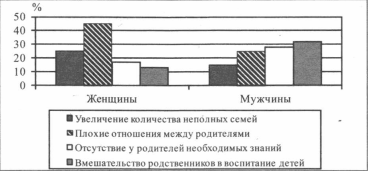
Решение
Ответ: 25