Задача 4641 Металлический проводник подвешен на...
Условие
1) растяжение пружинок увеличится
2) растяжение пружинок уменьшится
3) растяжение пружинок может увеличиться, может уменьшиться
4) растяжение пружинок не изменится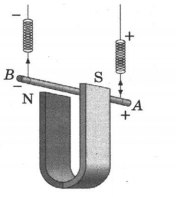
Решение
В магнитном поле постоянного магнита на проводник дополнительно будет действовать сила Ампера. Учитывая, что линии магнитного поля направлены от северного полюса магнита к южному, а электрический ток направлен от « + » к *-*, по правилу левой руки находим, что сила Ампера для рассматриваемого случая направлена вертикально вверх. Сила упругости уменьшится на величину, равную модулю силы Ампера. Следовательно, уменьшится и растяжение пружинок.
Ответ: 2