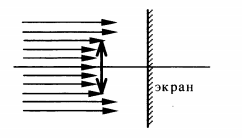
Пучок параллельных световых лучей падает нормально на тонкую собирающую линзу диаметром 6 см и оптической силой 5 дптр (см. рисунок). Экран освещен неравномерно. Выделяется более освещенная часть экрана (в форме кольца). Рассчитайте внутренний диаметр светлого кольца, создаваемого на экране. Экран находится на расстоянии 50 см от линзы. Ответ в см.
физика 10-11 класс
22057
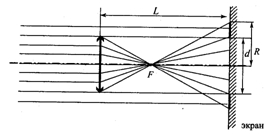
Лучи, падающие на линзу, соберутся в ее заднем главном фокусе, а затем разойдутся из него конусом и попадут на экран, образуя на нем светлый круг радиусом R. Из подобия треугольников следует, что
(d/2) / F = R / (L-F), где F =1/D = 20 см – фокусное расстояние линзы.
Отсюда R = (d/2)*((L-F)/F) = 4.5 см
Светлое кольцо возникает на экране там, где на экран попадают лучи, прошедшие линзу, и лучи из первичного пучка, не попавшие на линзу. Внешний диаметр этого кольца равен 2R, а его внутренний диаметр равен 6 см.
Ответ: 9
Вопросы к решению (3)
Длина, посмотрите на рисунок
почему вы нашли внешний диаметр, когда просят найти внутренний

