Задача 3316 В одном из заданий на конкурсе...
Условие
а) Удастся ли выполнить задание, если в отделе 40 сотрудников и все должны получить поровну?
б) Удастся ли выполнить задание, если ведущему специалисту надо выдать 80 000 рублей, а остальное поделить поровну на 80 сотрудников?
в) При каком наибольшем количестве сотрудников в отделе задание удастся выполнить при любом распределении размеров премий?
Решение
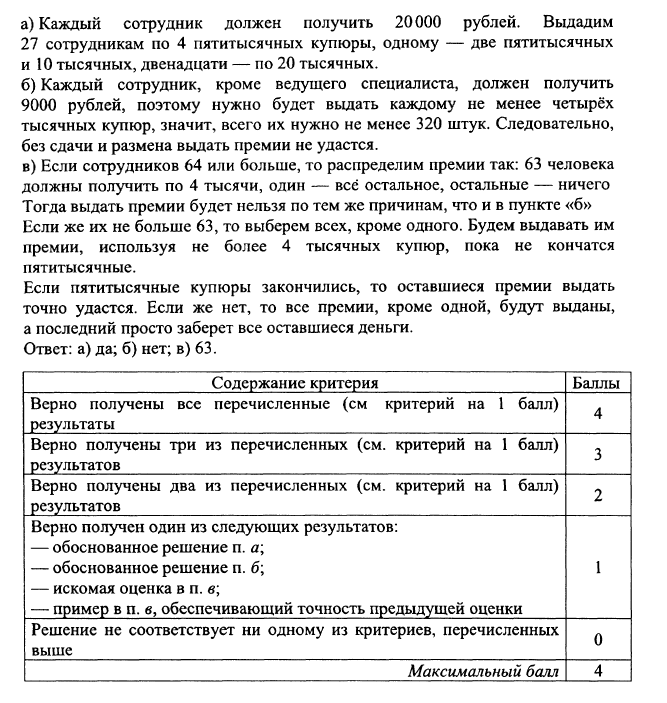
Ответ: да, нет, 63