Задача 12764 11) log(sqrt(2))sqrt(2x^4+20) =...
Условие
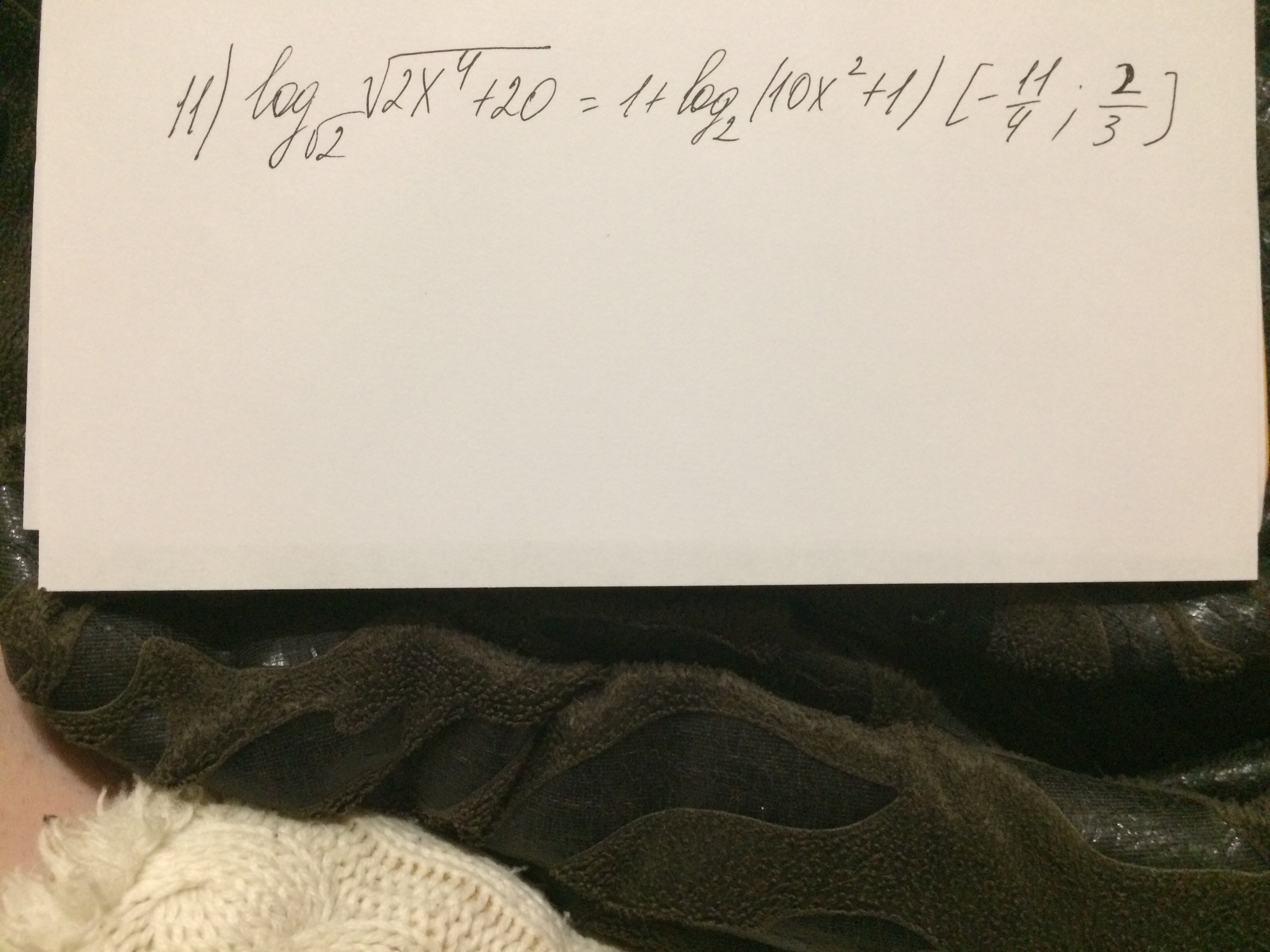
математика 10-11 класс
1241
Решение
★
log_(sqrt(2)sqrt(2x^4+20)=
=log_(2)sqrt(2x^4+20)/log_(2)sqrt(2)=
=log_(2)sqrt(2x^4+20)/(1/2)=2 log_(2)sqrt(2x^4+20)=
=log_(2)(sqrt(2x^4+20))^2=log_(2)(2x^4+20)
1=log_(2)2
log_(2)(2x^4+20)=log_(2)2+log_(2)(10x^2+1)
Cумму логарифмов заменим логарифмом произведения
log_(2)(2x^4+20)=log_(2)2*(10x^2+1);
2x^4+20=2*(10x^2+1);
2x^4-20x^2+18=0;
x^4-10x^2+9=0
D=100-36=64
x^2=1 или х^2=9
x_(1)=-1 > -11/4; x_(2)=1 > 2/3;x_(3)=-3 < -11/4; x_(4)=2 > 2/3
x=-1 принадлежит указанному промежутку