Формулы сложения cos(α±β) и sin(α±β)
Теорема: Для любых α и β справедливо равенство cos(α+β) = cosαcosβ – sinαsinβ.
Доказательство:
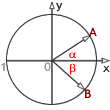
Чтобы получить эту формулу рассмотрим единичный тригонометрическую окружность с двумя радиус векторами OA и OB, соответствующими углам α и β.
По определению тригонометрических функций координаты векторов: ОА (cos α, sin α) и ОВ (cos β, sin β). Вычислим скалярное произведение этих векторов: ОА × ОВ = |ОА| × |ОВ| × cos (α+β) = cos (α+β)
Вычислим скалярное произведение векторов через координаты: ОА × ОВ = cos α cos β – sin α sin β. Так получается искомая формула: cos(α + β) = cos α cos β – sin α sin β.
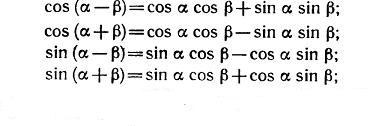
Доказательство:
Чтобы получить эту формулу рассмотрим единичный тригонометрическую окружность с двумя радиус векторами OA и OB, соответствующими углам α и β.
По определению тригонометрических функций координаты векторов: ОА (cos α, sin α) и ОВ (cos β, sin β). Вычислим скалярное произведение этих векторов: ОА × ОВ = |ОА| × |ОВ| × cos (α+β) = cos (α+β)
Вычислим скалярное произведение векторов через координаты: ОА × ОВ = cos α cos β – sin α sin β. Так получается искомая формула: cos(α + β) = cos α cos β – sin α sin β.
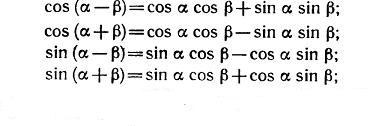

Просмотры: 2772 |
Статью добавил: SashaShevcova |
Категория: математика
☰ Меню