Принятые обозначения. Некоторые свойства параллельных проекций.
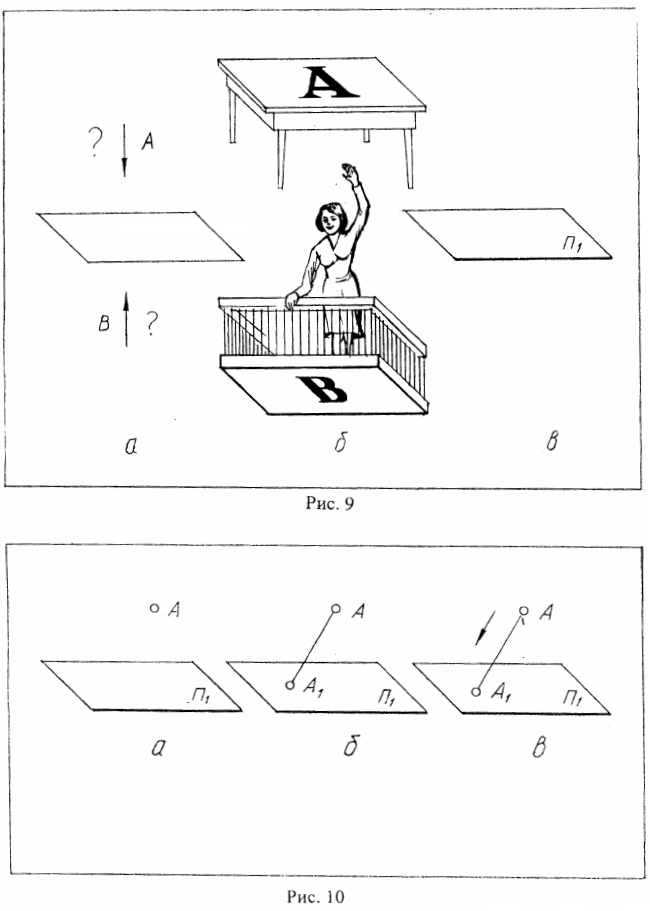
Что показано на рис.9а? Ответов, как правило, два: это параллелограмм; это горизонтальная плоскость. Оба ответа правильны. Если выбрать последний, то можно задать еще один вопрос, быть может, для некоторых неожиданный; откуда видна плоскость - сверху или снизу? Если это стол, то его крышка обычно видна сверху, ибо находится на высоте примерно 80 см. от стола. Если это балкон, то та же плоскость просматривается снизу /рис.9б/. Вот почему всякий раз, глядя на изображение, анализируйте его и пытайтесь представить во всем многообразии. Это поможет развитию у вас пространственных представлений. В практике начертательной геометрии горизонтальную плоскость значительно чаще изображают с просмотром сверху. Для того, чтобы подчеркнуть это, переднюю линию фигуры, ограничивающей плоскость, хорошо показывать чуть толще других /рис.9в/. Плоскости проекций в пашем курсе будем обозначать буквой П. Эта прописная буква тг, по этому будем произносить ее как пи. На чертеже может быть несколько плоскостей проекций. В зависимости от положения, каждой из них присваивается своя порядковая цифра (1,2,3 и т.д.). Горизонтальной плоскости проекций присвоена порядковая цифра 1, которая ставится рядом с буквой П. (например,П1).
Представим себе, что над горизонтальной плоскостью проекций /рис. 10а/ расположена точка. Если точке в ходе рассуждения отводится определенная самостоятельная роль, если требуется обратить на нее внимание и выделить ее на чертеже, то точку изображают кружочком, диаметр которого в два раза превышает толщину основной линии. Внутри кружочка линии не проводятся. Точки обозначают буквами латинского алфавита - А, В, С и т.д.
Проведем через точку А прямую произвольного наклона. Если она не параллельна плоскости П1, то рано или поздно пересечет ее. Точка пересечения прямой с плоскостью П1 является горизонтальной проекцией точки А. Проекция тоже обозначается буквой А1, но к обозначению прибавляется индекс той плоскости, на которую производилось проецирование, т.е. А1 /рис. 106/. Однако через точку А можно провести бесчисленное множество прямых, не параллельных П1, поэтому без указания направления проецирования у точки может быть бесчисленное множество проекций на плоскость, при заданном направлении проецирования - только одно /рис. 10в/.
Отсюда следует одно из свойств параллельных проекций: при заданном направлении проецирования у точки может быть только одна проекция на плоскость. Рассмотрим некоторые другие свойства, наиболее важные для данного курса.
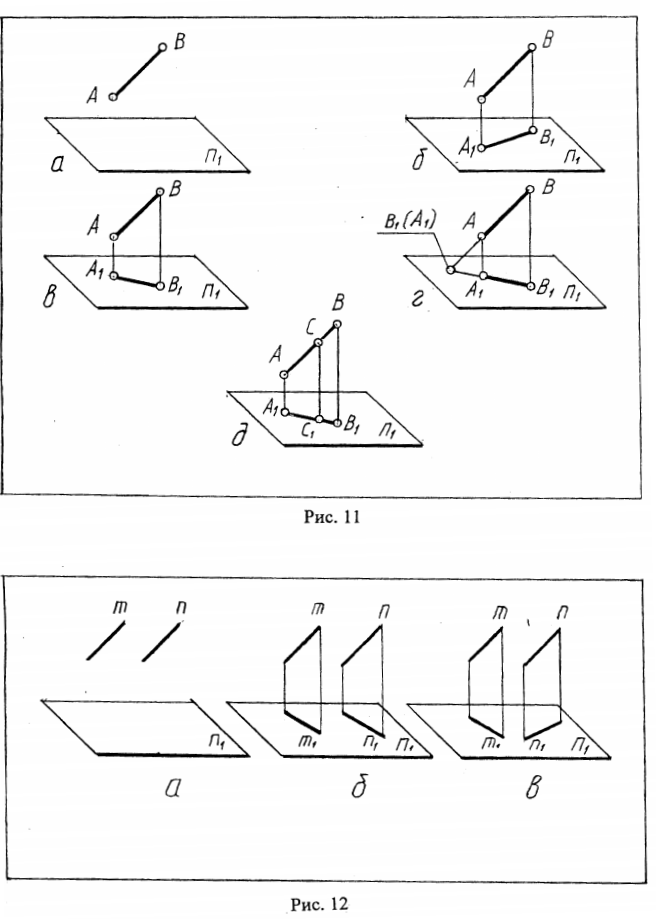
Представим себе отрезок АВ, расположенный над плоскостью П1 /рис.11а/. Попытайтесь представить, какая точка - А и В выше над плоскостью? Разве это плохо видно, что вы так медлите с ответом? Тогда подумайте, какая из этих точек к нам ближе?... Вы правы, ни на один из этих вопросов нельзя дать ответа, пока не будут известны проекции точек А и В на плоскость П1. Если AA1 больше, чем ВВ1, то точка А выше над плоскостью П1 и ближе к зрителю /рис.116/. Если же ВВ1 больше, чем АА1 то над плоскостью выше расположена точка В и она ближе к зрителю, чем точка А /рис.11 в/. Попытайтесь представить, где должны находиться А1 и В1 чтобы сами точки А и В располагались на одинаковом расстоянии от нас? Правильно, на одинаковом расстоянии от оси X. На рис.11/6, в/ отрезки А1В1 являются проекциями отрезка АВ. При этом направление проецирования не только параллельное, но и прямоугольное. Прямоугольное проецирование часто называют ортогональным (от греч. ortos -прямой). Значит, в общем случае проекцией отрезка на плоскость является отрезок. Дополнительно отметим следующее. Если отрезок АВ будет проецироваться на плоскость П1 по направлению, параллельному ему самому, то проекцией отрезка будет точка. На рис.11г ее легко получить, продолжив АВ и A1В1 до их пересечения. Будем считать, что направление нашего взгляда совпадает с направлением проецирования. Тогда в обозначений точки, в которую вырождается проекция отрезка, на первом месте нужно написать В1. Но проекции точек А и В совпадают, поэтому вслед за В1 нужно написать A1. Эта часть обозначения заключается в скобки, т.к. в пространстве при заданном направлении проецирования точка В заслоняет собой точку А.
Таким образом:
а) в частном случае проекцией отрезка может быть точка:
б) обозначение заслоняемой точки заключается в скобки.
Произвольная точка С и ее проекция С1 делят отрезок АВ и его проекцию АВ в равном отношении /рис.11 д/.
Таким образом, отношение частей отрезка в пространстве равно отношению частей его проекции.
Проведем параллельно друг другу прямые тип /рис. 12а/. Можно но ли по рисунку утверждать, что они действительно параллельны? Отметим на каждой из них конечные точки и спроецируем полученные отрезки на П1. Если проекции этих отрезков m1 и n1 в свою очередь, параллельны друг другу /рис. 126/, можно утверждать, что m || n. Итак, если прямые параллельны, их проекции соответственно параллельны. Если m1 и n1 не параллельны друг другу, то прямые m и n скрещиваются /рис.12в/.
Представим себе, что над горизонтальной плоскостью проекций /рис. 10а/ расположена точка. Если точке в ходе рассуждения отводится определенная самостоятельная роль, если требуется обратить на нее внимание и выделить ее на чертеже, то точку изображают кружочком, диаметр которого в два раза превышает толщину основной линии. Внутри кружочка линии не проводятся. Точки обозначают буквами латинского алфавита - А, В, С и т.д.
Проведем через точку А прямую произвольного наклона. Если она не параллельна плоскости П1, то рано или поздно пересечет ее. Точка пересечения прямой с плоскостью П1 является горизонтальной проекцией точки А. Проекция тоже обозначается буквой А1, но к обозначению прибавляется индекс той плоскости, на которую производилось проецирование, т.е. А1 /рис. 106/. Однако через точку А можно провести бесчисленное множество прямых, не параллельных П1, поэтому без указания направления проецирования у точки может быть бесчисленное множество проекций на плоскость, при заданном направлении проецирования - только одно /рис. 10в/.

Отсюда следует одно из свойств параллельных проекций: при заданном направлении проецирования у точки может быть только одна проекция на плоскость. Рассмотрим некоторые другие свойства, наиболее важные для данного курса.
Представим себе отрезок АВ, расположенный над плоскостью П1 /рис.11а/. Попытайтесь представить, какая точка - А и В выше над плоскостью? Разве это плохо видно, что вы так медлите с ответом? Тогда подумайте, какая из этих точек к нам ближе?... Вы правы, ни на один из этих вопросов нельзя дать ответа, пока не будут известны проекции точек А и В на плоскость П1. Если AA1 больше, чем ВВ1, то точка А выше над плоскостью П1 и ближе к зрителю /рис.116/. Если же ВВ1 больше, чем АА1 то над плоскостью выше расположена точка В и она ближе к зрителю, чем точка А /рис.11 в/. Попытайтесь представить, где должны находиться А1 и В1 чтобы сами точки А и В располагались на одинаковом расстоянии от нас? Правильно, на одинаковом расстоянии от оси X. На рис.11/6, в/ отрезки А1В1 являются проекциями отрезка АВ. При этом направление проецирования не только параллельное, но и прямоугольное. Прямоугольное проецирование часто называют ортогональным (от греч. ortos -прямой). Значит, в общем случае проекцией отрезка на плоскость является отрезок. Дополнительно отметим следующее. Если отрезок АВ будет проецироваться на плоскость П1 по направлению, параллельному ему самому, то проекцией отрезка будет точка. На рис.11г ее легко получить, продолжив АВ и A1В1 до их пересечения. Будем считать, что направление нашего взгляда совпадает с направлением проецирования. Тогда в обозначений точки, в которую вырождается проекция отрезка, на первом месте нужно написать В1. Но проекции точек А и В совпадают, поэтому вслед за В1 нужно написать A1. Эта часть обозначения заключается в скобки, т.к. в пространстве при заданном направлении проецирования точка В заслоняет собой точку А.
Таким образом:
а) в частном случае проекцией отрезка может быть точка:
б) обозначение заслоняемой точки заключается в скобки.
Произвольная точка С и ее проекция С1 делят отрезок АВ и его проекцию АВ в равном отношении /рис.11 д/.
Таким образом, отношение частей отрезка в пространстве равно отношению частей его проекции.
Проведем параллельно друг другу прямые тип /рис. 12а/. Можно но ли по рисунку утверждать, что они действительно параллельны? Отметим на каждой из них конечные точки и спроецируем полученные отрезки на П1. Если проекции этих отрезков m1 и n1 в свою очередь, параллельны друг другу /рис. 126/, можно утверждать, что m || n. Итак, если прямые параллельны, их проекции соответственно параллельны. Если m1 и n1 не параллельны друг другу, то прямые m и n скрещиваются /рис.12в/.

Просмотры: 2209 |
Статью добавил: slava191 |
Категория: начертательная_геометрия
☰ Меню