• Окружность


• Эллипс


• Гипербола


• Парабола


• Полярное уравнение эллипса, гиперболы и параболы

Окружность

Уравнение



определяет окружность радиуса R с центром C(a; B).

Если центр окружности совпадает с началом координат, то есть если a=0, B=0, то уравнение (1) принимает вид

Эллипс

Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами F1 и F2, расстояние между ними - через 2с. По определению эллипса 2a>2c или a>c.

Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид



где b=sqrt(a^2-c^2); очевидно, a>b. Уравнение вида (1) называется каноническим уравнением эллипса.



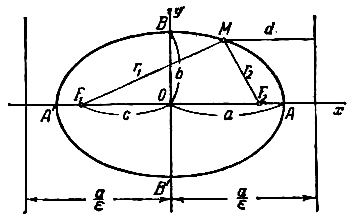
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса ABCD точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае b>a; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.

Число



где а - большая полуось, называется эксцентриситетом эллипса. Очевидно, ε<1 (для окружности ε=0 ). Если М(x; y) - произвольная точка эллипса, то отрезки F1M=r1 и F2M=r2 (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам



Если эллипс определен уравнением (1) и a>b, то прямые



называются директрисами эллипса (если b>a, то директрисы определяются уравнениями y=-b/ε, y=b/ε)

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:

Гипербола

Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через 2а. Фокусы гиперболы обозначают буквами F1 и F2, расстояние между ними - через 2с. По определению гиперболы 2a<2c, или a
Пусть дана гипербола. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид

x^2/a^2 - y^2/b^2 = 1

где b=sqrt(c^2 - a^2). Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы ABCD точки А’ и А.



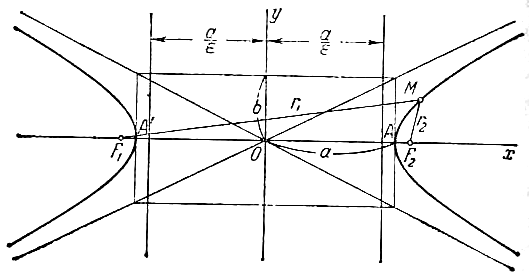
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.

Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть

y=(b/a)x, y=-(b/a)x

Уравнение

-x^2/a^2 + y^2/b^2 = 1 (2)

определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.

Две гиперболы, которые определяются уравнениями

x^2/a^2 - y^2/b^2 = 1, -x^2/a^2 + y^2/b^2 = 1

в одной и той же системе координат, называются сопряженными.

Гипербола с равными полуосями (a=b) называется равносторонней; ее каноническое уравнение имеет вид

x^2 - y^2 = a^2

Число

ε = c/a

где а - расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы ε > 1. Если М(x; y) - произвольная точка гиперболы, то отрезки F1M и F2M (см. рис.) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам

r1 = εx + a, r2 = εx - a

фокальные радиусы точек левой ветви - по формулам

r1 = -εx - a, r2 = -εx - a

Если гипербола задана уравнением (1), то прямые, определяемые уравнениями

x = -a/ε, x = a/ε

называются ее директрисами (см. рис.). Если гипербола задана уравнением (2), то директрисы определяются уравнениями

y = -b/ε, y = b/ε

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентрисистету гиперболы:

r/d = ε

ЗАДАЧА 3707 Эксцентриситет гиперболы e=2, фокальный

Эксцентриситет гиперболы e=2, фокальный радиус ее точки М, проведенный из некоторого фокуса, равен 16. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы. Смотреть решение...

ЗАДАЧА 3708 Эксцентриситет гиперболы e=3/2, центр ее

Эксцентриситет гиперболы e=3/2, центр ее лежит в начале координат, одна из директрис дана уравнением x=-8. Вычислить расстояние от точки М1 гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе. Смотреть решение...

Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

y^2 = 2px (1)

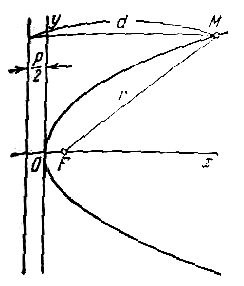
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

x = -p/2

Фокальный радиус произвольной точки М(x; y) параболы (то есть длина отрезка F(M) может быть вычислен по формуле

r = x + p/2

Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат - с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

y^2 = -2px (2)

В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

x^2 = 2py (3)

если она лежит в верхней полуплоскости (рис.), и

x^2 = -2py (4)

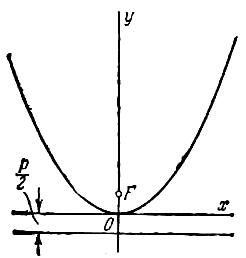
если в нижней полуплоскости (рис.)



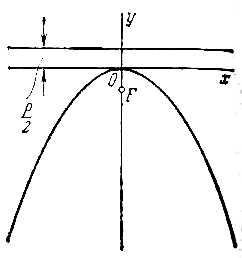
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

ЗАДАЧА 3709 Вычислить фокальный радиус точки М

Вычислить фокальный радиус точки М параболы y^2 = 20x, если абсцисса точки М равна 7. Смотреть решение...

ЗАДАЧА 3710 Составить уравнение параболы, если даны

Составить уравнение параболы, если даны ее фокус F(4; 3) и директриса x-5=0 Смотреть решение...

Полярное уравнение эллипса, гиперболы, параболы

Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы, имеет вид

p = p/(1 - εcosθ) (1)

где p, θ - полярные координаты произвольной точки линии, р - фокальный параметр (половина фокальной хорды линии, перпендикулярной к ее оси), ε - эксцентриситет (в случае параболы ε = 1). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокусу директрисы.

ЗАДАЧА 3711 Дано уравнение эллипса x^2/a^2 + y^2/b^2

Дано уравнение эллипса x^2/a^2 + y^2/b^2 = 1. Составить его полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в центре эллипса. Смотреть решение...

ЗАДАЧА 3712 Дано уравнение гиперболы x^2/a^2 -

Дано уравнение гиперболы x^2/a^2 - y^2/b^2 = 1. Составить ее полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в центре гиперболы. Смотреть решение...

ЗАДАЧА 3713 Дано уравнение параболы y^2 = 2px.

Дано уравнение параболы y^2 = 2px. Составить ее полярное уравнение при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в вершине параболы. Смотреть решение...