• Предел последовательности


• Предел функции


• Теоремы о пределах


• Таблица известных пределов

Предел последовательности

В основе математического анализа лежит важнейшее понятие предела переменной величины. Рассмотрим это понятие на простейшем случае, когда переменной величиной является функция целочисленного аргумента, т.е. числовая последовательность.

Пусть задана некоторая бесконечная числовая последовательность {Xn}. Изобразив ее члены точками на числовой прямой, в некоторых случаях можно заметить, что с возрастанием номера членов последовательности эти точки начинают все ближе и ближе «подбираться» к одной точке, изображающей некоторое постоянное число «a» (не обязательно являющееся членом последовательности), т.е. расстояние на числовой прямой между числом «a» и членами последовательности становится все меньше. Известно, что расстояние на числовой прямой между точками, изображающими числа x и a, равно |x-a|,
system{x-a, если x больше или равно a; a-x, если x < a}

Определение. Число a называют пределом бесконечной числовой последовательности {Xn}, если для всякого числа ε>0 (как бы мало оно ни было) можно указать такой номер M, зависящий от ε (M=M(ε)), начиная с которого все члены Xn с номерами большими M(n>M), будут удовлетворять неравенству |Xn-a| < ε (т.е. окажутся в ε-окрестности точки а)

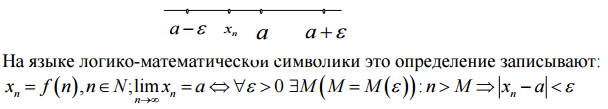
Предел функции.

Несмотря на тот факт, что последовательность - частный случай функции (функция целочисленного аргумента), определение предела функции в общем смысле будет несколько другим, так как аргумент x у функции y=f(x) может стремиться к любому числу (тогда как у последовательности n стремится только к бесконечности). Пусть функция y = f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а.

Определение. Число b называют пределом функции у = f(X) при x—>а, если для всякого числа ε>0 (как бы мало оно ни было) можно указать такое число δ(δ = δ(ε))>0, что для всех значений х, удовлетворяющих неравенству |x-a| < δ, будет выполняться неравенство |f(x)-b| < ε.


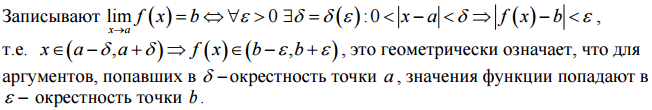
Рассмотрим понятия односторонних пределов функции

Определение. Если у = f(x) стремится к пределу b при x—>a только с одной стороны (справа (x>a)или слева (хпределом функции у = f(х) в точке x = a справа или слева и обозначают:


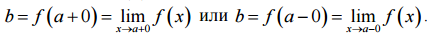
Существует понятие о бесконечном пределе, хотя это и означает отсутствие предела как числа.

Определение. lim(х) = ±∞, если для любого числа М>0 можно указать такое число δ(δ = δ(M)), что для всех значений х, удовлетворяющих неравенству 0 < |x-a| < δ, будет выполняться неравенство |f(x)| > М.


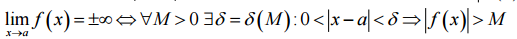
Теоремы о пределах



Таблица известных пределов

ЗАДАЧА 3700 Вычислить

Вычислить lim(n->беск)(sqrt(n+2)-sqrt(n)) Смотреть решение...

ЗАДАЧА 3701 Вычислить lim(n->беск)((2n-1)/(5n+7)

Вычислить lim(n->беск)((2n-1)/(5n+7) - (1+2n^3)/(2+5n^3)) Смотреть решение...