• Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми


• Неполные уравнения прямой. Уравнение прямой в отрезках


• Нормальное уравнение прямой. Расстояние от точки до прямой


• Уравнение пучка прямых


• Полярное уравнение прямой

Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.

Уравнение вида

называется общим уравнением прямой.

Угол альфа, определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:





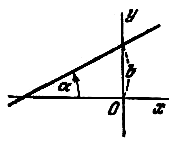
Уравнение y=kx+b называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением



то ее угловой коэффициент определяется по формуле



Уравнение y-y0=k(x-x0) является уравнением прямой, которая проходит через точку M0(x0, y0) и имеет угловой коэффициент k.

Если прямая проходит через точки M1(x1, y1), M2(x2, y2), то ее угловой коэффициент определяется по формуле

k=(y2-y1)/(x2-x1)

Уравнение

(x-x1)/(x2-x1) = (y-y1)/(y2-y1)

является уравнением прямой, проходящей через две точки M1(x1, y1), M2(x2, y2)


Если известны угловые коэффициенты k1 и k2 двух прямых, то один из углов φ между этими прямыми определяется по формуле



Признаком параллельности двух прямых является равенство их угловых коэффициентов:



Признаком перпендикулярности двух прямых является соотношение

Неполные уравнения прямой. Совместное исследование уравнение двух и трех прямых. Уравнение прямой в отрезках

Если в общем уравнении прямой



один или два из трех коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:

1). С=0; уравнение имеет вид Ax+By=0 и определяет прямую, проходящую через начало координат.

2). В=0 (А ≠ 0); уравнение имеет вид Ax+C=0 и определяет прямую, перпендикулярную к оси Ох. Это уравнение может быть записано в виде х=а, где a=-C/A является величиной отрезка, который отсекает прямая на оси Ох, считая от начала координат.

3). В=0, С=0 (А ≠ 0); уравнение может быть записано в виде х=0 и определяет ось ординат.

4). А=0 (В ≠ 0); уравнение имеет вид By+C=0 и определяет прямую, перпендикулярную к оси Оу. Это уравнение может быть записано в виде y=b, где b=-C/B является величиной отрезка, который отсекает прямая на оси Оу, считая от начала координат.

5). А=0, С=0 (В ≠ 0); уравнение может быть записано в виде у=0 и определяет ось абсцисс.

Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду



где a=-C/A, b=-C/B суть величины отрезков, которые отсекает прямая на координатных осях.

Уравнение (2) называется уравнением прямой «в отрезках».

Если две прямые даны уравнениями



то могут представиться три случая:


а). A1/A2 ≠ B1/B2 - прямые имеют одну общую точку;

б). A1/A2 = B1/B2 ≠ C1/C2 - прямые параллельны;

в). A1/A2 = B1/B2 = C1/C2 - прямые сливаются, то есть оба уравнения определяют одну и ту же прямую.

Нормальное уравнение прямой. Расстояние от точки до прямой

Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.

Если альфа - полярный угол нормали, р - длина отрезка OP(рис.), то уравнение данной прямой может быть записано в виде



уравнение этого вида называется нормальным.



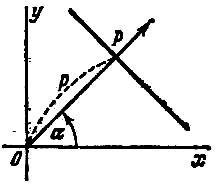
Пусть дана какая-нибудь прямая и произвольная точка M*; обозначим через d расстояние от точки М* до данной прямой. Отклонением δ точки M* от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и -d, если данная точка и начало координат расположены по одну сторону от данной прямой. (Для точек, лежащих на самой прямой, δ=0). Если даны координаты x*, y* точки M* и нормальное уравнение прямой xcosa + ysina - p = 0, то отклонение δ точки M* от этой прямой может быть вычислено по формуле



Таким образом, чтобы найти отклонение какой-нибудь точки M* от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки M*. Полученное число будет равно искомому отклонению.

Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль: d=|δ|.

Если дано общее уравнение прямой Ax+By+C=0, то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель μ, определяемый формулой



Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

Уравнение пучка прямых

Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром в S.

Если A1x+B1y+C1=0 и A2x+B2y+C2=0 - уравнения двух прямых, пересекающихся в точке S, то уравнение



где альфа, бета - какие угодно числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S.

Более того, в уравнении (1) числа альфа, бета всегда возможно подобрать так, чтобы оно определило любую (заранее назначенную) прямую, проходящую через точку S, иначе говоря, любую прямую пучка с центром S. Поэтому уравнение вида (1) называется уравнением пучка (с центром в S).

Если альфа ≠ 0, то, деля обе части уравнения (1) на альфа и полагая бета/альфа = лямбда, получим



Этим уравнением можно определить любую прямую пучка с центром S, кроме той, которая соответствует альфа=0, то есть кроме прямой

Полярное уравнение прямой

Прямая, проведенная через полюс перпендикулярно к данной прямой, называется ее нормалью. Обозначим буквой Р точку, в которой нормаль пересекает прямую; установим на нормали положительное направление от точки О к точке Р. Угол, на который нужно повернуть полярную ось до наложения ее на отрезок OP, будем называть полярным углом нормали.