Теория к заданию 12 ЕГЭ по Математике ''Наибольшее и наименьшее значение функций''

В этой статье я расскажу про алгоритм поиска наибольшего и наименьшего значения функции, точек минимума и максимума.

Из теории нам точно пригодится таблица производных и правила дифференцирования. Все это есть в этой табличке:



Алгоритм поиска наибольшего и наименьшего значения.

Мне удобнее объяснять на конкретном примере. Рассмотрим:



Шаг 1. Берем производную.

y' = (x^5+20x^3–65x)' = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Шаг 2. Находим точки экстремума.

Точкой экстремума мы называем такие точки, в которых функция достигает своего наибольшего или наименьшего значения.

Чтобы найти точки экстремума, надо приравнять производную функции к нулю (y' = 0)

5x^4 + 60x^2 - 65 = 0

Теперь решаем это биквадратное уравнение и найденные корни есть наши точки экстремума.

Я решаю такие уравнения заменой t = x^2, тогда 5t^2 + 60t - 65 = 0.

Сократим уравнение на 5, получим: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

t_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

t_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Делаем обратную замену x^2 = t:

x_(1 и 2) = ±sqrt(1) = ±1
x_(3 и 4) = ±sqrt(-13) (исключаем, под корнем не может быть отрицательных чисел, если конечно речь не идет о комплексных числах)

Итого: x_(1) = 1 и x_(2) = -1 - это и есть наши точки экстремума.

Шаг 3. Определяем наибольшее и наименьшее значение.

Метод подстановки.

В условии нам был дан отрезок [b][–4;0][/b]. Точка x=1 в этот отрезок не входит. Значит ее мы не рассматриваем. Но помимо точки x=-1 нам также надо рассмотреть левую и правую границу нашего отрезка, то есть точки -4 и 0. Для этого подставляем все эти три точки в исходную функцию. Заметьте исходную - это ту, которая дана в условии (y=x^5+20x^3–65x), некоторые начинают подставлять в производную...

y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44[/b]
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Значит наибольшее значение функции это [b]44[/b] и достигается оно в точки [b]-1[/b], которая называется точкой максимума функции на отрезке [-4; 0].

Мы решили и получили ответ, мы молодцы, можно расслабиться. Но стоп! Вам не кажется, что считать y(-4) как-то слишком сложно? В условиях ограниченного времени лучше воспользоваться другим способом, я называю его так:

Через промежутки знакопостоянства.

Находятся эти промежутки для производной функции, то есть для нашего биквадратного уравнения.

Я делаю это следующим образом. Рисую направленный отрезок. Расставляю точки: -4, -1, 0, 1. Не смотря на то, что 1 не входит в заданный отрезок, ее все равно следует отметить для того, чтобы корректно определить промежутки знакопостоянства. Возьмем какое-нибудь число во много раз больше 1, допустим 100, мысленно подставим его в наше биквадратное уравнение 5(100)^4 + 60(100)^2 - 65. Даже ничего не считая становится очевидно, что в точке 100 функция имеет знак плюс. А значит и на промежутки от 1 до 100 она имеет знак плюс. При переходе через 1 (мы идем справа налево)функция сменит знак на минус. При переходе через точку 0 функция сохранит свой знак, так как это лишь граница отрезка, а не корень уравнения. При переходе через -1 функция опять сменит знак на плюс.



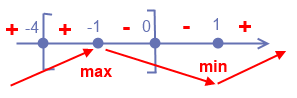
Из теории мы знаем, что там, где производная функции (а мы именно для нее это и чертили) меняет знак с плюса на минус (точка -1 в нашем случае) функция достигает своего локального максимума (y(-1)=44, как была посчитано ранее) на данном отрезке (это логически очень понятно, функция перестала возрастать, так как достигла своего максимума и начала убывать).

Соответственно, там где производная функции меняет знак с минуса на плюс, достигается локальный минимум функции. Да, да, мы также нашли точку локального минимума это 1, а y(1) - это минимальное значение функции на отрезке, допустим от -1 до +∞. Обратите огромное внимание, что это лишь ЛОКАЛЬНЫЙ МИНИМУМ, то есть минимум на определенном отрезке. Так как действительный (глобальный) минимум функция достигнет где-то там, в -∞.

На мой взгляд первый способ проще теоретически, а второй проще с точки зрения арифметических действий, но намного сложнее с точки зрения теории. Ведь иногда бывают случаи, когда функция не меняет знак при переходе через корень уравнения, да и вообще можно запутаться с этими локальными, глобальными максимумами и минимумами, хотя Вам так и так придется это хорошо освоить, если вы планируете поступать в технический ВУЗ (а для чего иначе сдавать профильное ЕГЭ и решать это задание). Но практика и только практика раз и навсегда научит Вас решать такие задачи. А тренироваться можете на нашем сайте. Вот здесь.

Если появились какие-то вопросы, или что-то непонятно - обязательно спросите. Я с радостью Вам отвечу, и внесу изменения, дополнения в статью. Помните мы делаем этот сайт вместе!